( (本题满分12分)已知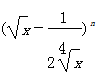 的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.
的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.
已知函数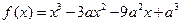
 .
.
(1)设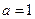 ,求函数
,求函数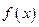 的极值;
的极值;
(2)若 ,且当
,且当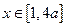 时,
时,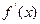
 12a恒成立,试确定
12a恒成立,试确定 的取值范围
的取值范围
已知函f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)="f(x)+" f′\(x)是奇函数。
(1)求f(x)的表达式;
(2)试论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值。
函数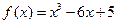 ,
,
⑴求函数 的单调区间和极值;
的单调区间和极值;
⑵若关于 的方程
的方程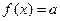 有三个不同的实根,求实数
有三个不同的实根,求实数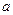 的取值范围
的取值范围
已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=— 1.
1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值点还是极大值点,并说明理由
圆柱形容器,其底面直径为2m,深度为1 m,盛满液体后以0.01m3/s的速率放出,求液面高度的变化率