已知二次函数的图象与x轴只有一个交点A(-2,0)、与y轴的交点为B(0,4),且其对称轴与y轴平行.求该二次函数的解析式,并在所给坐标系中画出它的大致图象;
在二次函数位于A、B两点之间的图象上取一点M,过点M分别作x轴、y轴的垂线,垂足分别为点C、D.求矩形MCOD的周长的最小值和此时的点M的坐标.

解不等式组: 
计算: ;
;
如图,抛物线F: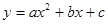 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: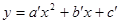 ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.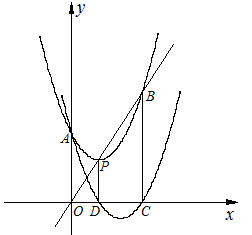
⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了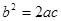
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
如图15,在△ABC和△PQD中,AC =" k" BC,DP =" k" DQ,∠C =∠PDQ,D、E分别是AB、AC的中点,点P在直线BC上,连结EQ交PC于点H.猜想线段EH与AC的数量关系,并证明你的猜想.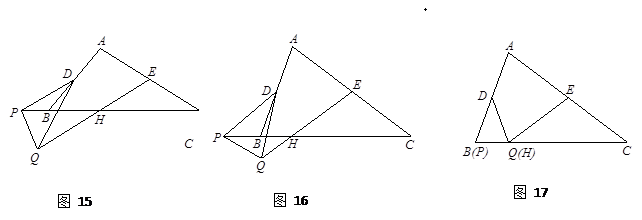
如图14,矩形ABCD中,AB = 6cm,AD = 3cm,点E在边DC上,且DE = 4cm.动点P从点A开始沿着A→B→C→E的路线以2cm/s的速度移动,动点Q从点A开始沿着AE以1cm/s的速度移动,当点Q移动到点E时,点P停止移动.若点P、Q同时从点A同时出发,设点Q移动时间为t (s),P、Q两点运动路线与线段PQ围成的图形面积为S (cm2),求S与t的函数关系式.