如图,设P是圆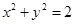 上的动点,点
上的动点,点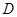 是
是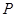 在
在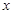 轴上的投影,
轴上的投影,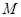 为线段PD上
为线段PD上 一点,且
一点,且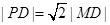 .点
.点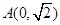 、
、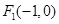 .
.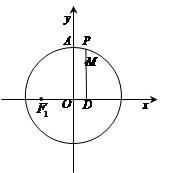
(1)设在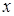 轴上存在定点
轴上存在定点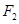 ,使
,使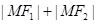 为定值,试求
为定值,试求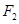 的坐标,并指出定值是多少?
的坐标,并指出定值是多少?
(2)求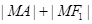 的最大值,并求此时点
的最大值,并求此时点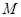 的坐标.
的坐标.
设 是公差不为0的等差数列
是公差不为0的等差数列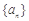 的前
的前 项和,已知
项和,已知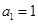 ,且
,且 成等比数列;
成等比数列;
(1)求数列 的通项公式;
的通项公式;
(2)求数列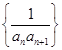 的前
的前 项和。
项和。
在△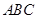 中,角
中,角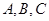 所对的边分别为
所对的边分别为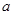 、
、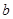 、
、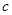 ,若
,若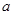 、
、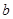 是方程
是方程 的两根,且
的两根,且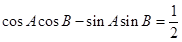 ;
;
(1)求角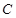 的大小;
的大小;
(2)求边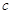 的长度;
的长度;
(3)求 的面积。
的面积。
(1)已知 ,求
,求 的值;
的值;
(2)已知 都是锐角,
都是锐角, ,求
,求 的值.
的值.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE.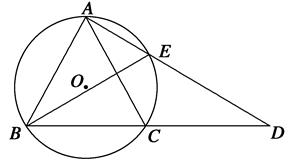
求证:(1)BE=DE;
(2)∠D=∠ACE.
如图,已知PA与⊙O相切,A为切点,PBC为割线,D为⊙O上一点,AD、BC相交于点E.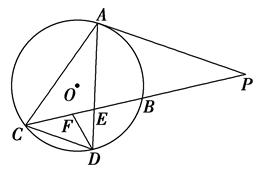
(1)若AD=AC,求证:AP∥CD;
(2)若F为CE上一点使得∠EDF=∠P,已知EF=1,EB=2,PB=4,求PA的长.