已知斜三棱柱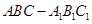 ,
, ,
, ,
,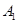 在底面
在底面 上的射影恰为
上的射影恰为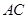 的中点
的中点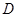 ,又知
,又知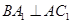 。
。
(I)求证: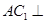 平面
平面 ;
;
(II)求二面角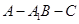 余弦值的大小。
余弦值的大小。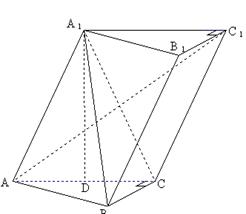
已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,求动圆圆心M的轨迹方程.
已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线y=
,直线y= x+1与椭圆相交于A、B两点,点M在椭圆上,
x+1与椭圆相交于A、B两点,点M在椭圆上, =
=
 +
+
 ,求椭圆的方程.
,求椭圆的方程.
已知椭圆的中心在原点,离心率为 ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数).
(1)求椭圆的方程;
(2)设Q是椭圆上的一点,且过点F、Q的直线l与y轴交于点M,若| |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率.
如图所示,点P是椭圆 =1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
=1上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
求适合下列条件的椭圆的标准方程:
(1)两个焦点坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0);
(3)经过P(-2 ,1),Q(
,1),Q( ,-2)两点.
,-2)两点.