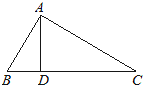
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1与∠2互补,判断HF与AB是否垂直,
并说明理由(填空).
解:垂直。理由如下:
∵DE⊥AC,AC⊥BC
∴∠AED=∠ACB=90º(垂直的意义)
∴DE∥BC( )
∴∠1=∠DCB( )
∵∠1与∠2互补(已知)
∴∠DCB与∠2互补
∴______∥_______( )
∴____________=∠CDB( )
∵CD⊥AB
∴∠CDB=90º
∴∠HFB="90º"
∴HF⊥AB
某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
| 普通间(元/人/天) |
豪华间(元/人/天) |
贵宾间(元/人/天) |
|
| 三人间 |
50 |
100 |
500 |
| 双人间 |
70 |
150 |
800 |
| 单人间 |
100 |
200 |
1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
如图,矩形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,OA=10、OC=8,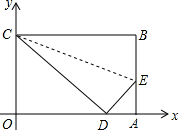
(1)如图,在AB上取一点E,使得△CBE沿CE翻折后,点B落在x轴上,记作点D.求点D的坐标;
(2)求折痕CE所在直线的解析式.
八年级三班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:
李小波:阿姨,您好!
售货员:同学,你好,想买点什么?
李小波:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB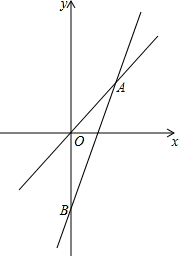
(1)求两个函数的解析式;
(2)直线AB交x轴于点C,求△AOC的面积;
(3)在x轴上存在一点p,使△AOP是等腰三角形,直接写出所有符合要求的点P的坐标.
如图,△ABC中,D是BC上的一点,若AB=10,BD=6,AD=8,AC=17,求△ABC的面积.