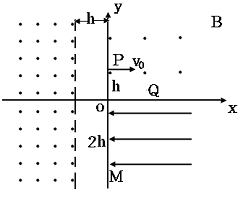
质量为m、电量为q的带电离子从P（0，h）点沿x轴正方向射入第一象限的匀强磁场中，磁感应强度为B，并沿着y轴负方向垂直进入匀强电场（电场方向沿x轴负方向），然后离子经过y轴上的M（0，－2h）点，进入宽度为h的无场区域，如图所示，再进入另一范围足够大的匀强磁场，最后回到P点。不计重力，试求：初速度v0
电场强度E
从P点出发到再次回到P点所用的时间
如图所示，在以O为圆心，半径为R=l0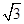
cm的圆形区域内，有一个水平方向的匀强磁场，磁感应强度大小为B="0." 10 T，方向垂直纸面向外．竖直平行放置的两个金属板A、K连在如右图所示的电路中．电源电动势E=" 91" V，内阻r=1．O，定值电阻
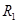=l0
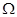，滑动变阻器
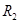的最大阻值为80 ,
、
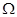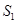为A、K板上的两个小孔，且,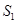、与O都在同一水平直线上，另有一水平放置的足够长的荧光屏D，O点跟荧光屏D之间的距离为H="3" R．比荷（带电粒子的电量与质量之比）为2．0×l0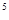
C/kg的带正电的粒子由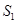进入电场后，通过向磁场中心射去，通过磁场后打到荧光屏D上．粒子进入电场的初速度、重力均可忽略不计．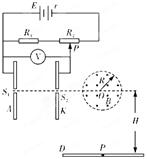
（1）如果粒子垂直打在荧光屏上的P点，电压表的示数为多大？
（2）调节滑动变阻器滑片P的位置，求粒子打到荧光屏的范围．
(12分)如图所示，在距水平地面高为0.4m处，水平固定一根长直光滑杆，杆上P处固定一定滑轮（大小不计），滑轮可绕水平轴无摩擦转动，在P点的右边，杆上套一质量m=3kg的滑块A。半径R=0.3m的光滑半圆形轨道竖直地固定在地面上，其圆心O在P点的正下方，在轨道上套有一质量m=3kg的小球B。用一条不可伸长的柔软细绳，通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内，滑块和小球均可看作质点，且不计滑轮大小的影响。现给滑块A施加一个水平向右、大小为60N的恒力F，求：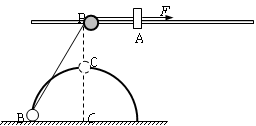 
（1）把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功。
（2）小球B运动到C处时所受的向心力的大小。
（3）小球B被拉到离地多高时滑块A与小球B的速度大小相等？
一辆汽车从静止开始匀加速开出，然后保持匀速运动，最后匀减速运动，直到停止．下表给m了不同时刻汽车的速度：
（l）汽车从开出到停止共经历的时间是多少？
（2）汽车在全程中的平均速度是多少？
普朗克常量h=6.63×l0 J．s，铝的逸出功 =6.72×10 J，现用波长 ="200" nm的光照射铝的表面（结果保留三位有效数字）．
①求光电子的最大初动能；
②若射出的一个具有最大初动能的光电子正对一个距离足够远且静止的电子运动，求在此运动过程中两电子电势能增加的最大值（除两电子间的相互作用以外的力均不计）．
用氦氖激光器进行双缝干涉实验，已知使用的双缝间距离d="0.1" mm，双缝到屏的距离 =6.0m，测得屏上干涉条纹中亮纹的间距是3.8 cm，氦氖激光器发出的红光的波长是多少？假如把整个装置放人折射率是 的水中，这时屏上的条纹间距是多少？