质谱分析技术已广泛应用于各前沿科学领域。汤姆孙发现电子的质谱装置示意如图，M、N为两块水平放置的平行金属极板，板长为L，板右端到屏的距离为D，且D远大于L，O’O为垂直于屏的中心轴线，不计离子重力和离子在板间偏离O’O的距离．以屏中心O为原点建立xOy直角坐标系，其中x轴沿水平方向，y轴沿竖直方向．设一个质量为m0、电荷量为q0的正离子以速度v0沿O’O的方向从O’点射入，板间不加电场和磁场时，离子打在屏上O点．若在两极板间加一沿+y方向场强为E的匀强电场，求离子射到屏上时偏离O点的距离y0；
假设你利用该装置探究未知离子，试依照以下实验结果计算未知离子的质量数．
上述装置中，保留原电场，再在板间加沿-y方向的匀强磁场．现有电荷量相同的两种正离子组成的离子流，仍从O’点沿O’O方向射入，屏上出现两条亮线．在两线上取y坐标相同的两个光点，对应的x坐标分别为3.24mm和3.00mm，其中x坐标大的光点是碳12离子击中屏产生的，另一光点是未知离子产生的．尽管入射离子速度不完全相同，但入射速度都很大，且在板间运动时O’O方向的分速度总是远大于x方向和y方向的分速度（本题中洛伦兹力可近似看成恒力）．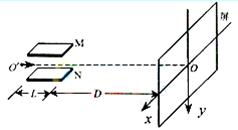
一列简谐横波由质点A向质点B传播。已知A、B两点相距4 m，这列波的波长大于2 m而小于20 m，下图表示在波的传播过程中A、B两质点的振动的图像，求波的传播速度。
一个单摆在质量为m1、半径为R1的星球上做周期为T1的简谐运动，在质量为m2、半径为R2的星球上做周期为T2的简谐运动。求T1与T2之比。
一滴露水的质量约是9×10-5g。它含有多少个水分子。（取阿伏伽德罗常数NA=6.0×1023mol-1，水的摩尔质量是18g/mol）
如图所示，R为电阻箱，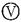
为理想电压表．当电阻箱读数为R1=2Ω时，电压表读数为U1=4V；当电阻箱读数为R2=5Ω时，电压
表读数为U2=5V．求：
（1）电源的电动势E和内阻r
（2）当电阻箱R读数为多少时，电源的输出功率最大?最大值Pm为多少?
如图所示，电源的电动势E=110V，电阻R1=21Ω，电动机绕组的电阻R0=0.5Ω，电键S1始终闭合。当电键S2断开时，电阻R1的电功率是525W；当电键S2闭合时，电阻R1的电功率是336W，求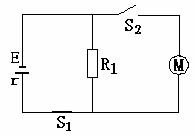
（1）电源的内电阻；
（2）当电键S2闭合时流过电源的电流和电动机的输出的功率。