如图所示，在E=103V/m的竖直匀强电场中，有一光滑的半圆形绝缘轨道QPN与一水平绝缘轨道MN连接，半圆形轨道平面与电
场线平行，P为QN圆弧的中点，其半径R=40cm，一带正电q=10-4C的小滑块质量m=10g，与水平轨道间的动摩擦因数μ=0.15，位于N 点右侧1.5m处，取g=10m/s2，求：
要使小滑块恰能运动到圆轨道的最高点Q，则滑块应以多大的初速度v0向左运动？
这样运动的滑块通过P点时对轨道的压力是多大？
|
如图所示，P、N是两个长为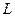
的平行板，它们相距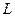，今有一个质量为
、带电量为
的正电荷以速度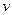
沿平行板面的方向贴着P板从一端打入。①如果板间加一个垂直于纸面向外的磁场后，该带电粒子可以打出平行板区域，试求磁场的磁感应强度B的取值范围；②如果板间加一个垂直于板面从P板指向N板的电场后，带电粒子可从板间射出，则所加电场的场强怎样取值？（带电粒子的重力不计）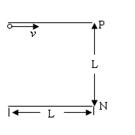
如图所示，在倾角为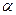
的光滑斜面上，垂直纸面放置一根长为
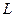、质量为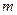
的直导体棒，当导体棒中通以垂直于纸面向里的电流
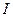并置于竖直向上的匀强磁场中时，导体棒恰好能静止在斜面上，试求该磁场的磁感应强度是多大？如果要保持导体棒在斜面上静止且要所加磁场的磁感应强度最小，则所加磁场的方向应该怎样？最小的磁感应强度多大？
某直流电动机提升重物的装置如图所示，已知电源提供的电压
，内阻不计，电机中的一切摩擦不计。当电机提升
的重物时，测得电路中的电流为
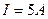，物体的提升速度是
，
①试求出电机的热功率和电动机线圈的电阻R；
②若电机提拉的物体过重而无法提起，此时电机内热功率又如何？（设电机不能被烧毁）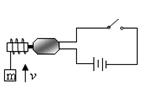
如图所示的电路中，已知电源的电动势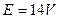
，内阻不详，
，
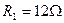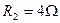。电阻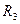
未知，将理想的安培表和伏特表接入电路中后，安培表的读数为1A，伏特表的读数为4V，试求出电源的内电阻和
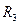的阻值。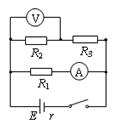
如图甲所示，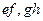
为水平放置的足够长的平行光滑导轨，导轨间距
，导轨左端连接一个R=2
的电阻，将一根质量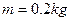
的金属棒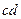
垂直地放置导轨上，且与导轨接触良好，导轨与
金属棒的电阻均不计，整个装置放在磁感强度B=2T的匀强磁场中，磁场方向垂直于导轨平面向下，现对金属棒施加一水平向右的拉力F，并保持拉力的功率恒为P=8W，使棒从静止开始向右运动。已知从金属棒开始运动直至达到稳定速度的过程中电阻R产生的热量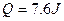
。试解答以下问题：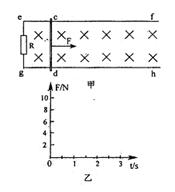
（1）金属棒达到的稳定速度是多少？
（2）金属棒从开始运动直至达到稳定速度所需的时间是多少？
（3）金属棒从开始运动直至达到稳定速度的过程中所产生的平均感应电动势可在什么数值范围内取值？
（4）在乙图中画出金属棒所受的拉力F随时间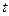
变化的大致图像。