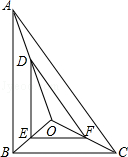
(本题12分)如图,两个同样大小的等边△ABC和△ACD,边长为a,它们拼成一个菱形ABCD,另一个足够大的等边△AEF绕点A旋转,AE与BC相交于点M,AF与CD相交于点N。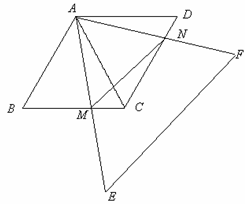
(1)证明:∠DAN=∠CAM;
(2)求四边形AMCN的面积;
(3)探索△AMN何时面积最小,并写出这个最小面积的值.
我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1,由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,通过复制形成的多边形中的任意相邻两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
(1)图1中标出的是一种可能的复制结果,小明发现△A∽△B,其相似比为 _________ .在图1的基础上继续复制下去得到△C,若△C的一条边上恰有11个小三角形(指有一条边在该边上的小三角形),则△C中含有 _________ 个小三角形;
(2)若△A是正三角形,你认为通过复制能形成的正多边形是 _________ ;
(3)请你用两次旋转和一次平移复制形成一个四边形,在图2的方框内画出草图,并仿照图1作出标记.
如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.
(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)
(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;
(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;
(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.
在△ABC中,AB=4,如图(1)所示,DE∥BC,DE把 ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
ABC分成面积相等的两部分,即SⅠ=SⅡ,求AD的长.
如图(2)所示,DE∥FG∥BC,DE、FG把△ABC分成面积相等的三部分,即SⅠ=SⅡ=SⅢ,求AD的长;
如图(3)所示,DE∥FG∥HK∥…∥BC,DE、FG、HK、…把△ABC分成面积相等的n部分,SⅠ=SⅡ=SⅢ=…,请直接写出AD的长.
如图1,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B运动,点Q从点B以2cm/s的速度沿BC边向点C运动,如果P、Q同时出发,设运动时间为ts,
(1)当t=2时,求△PBQ的面积;
(2)当t= 时,试说明△DPQ是直角三角形;
时,试说明△DPQ是直角三角形;
(3)当运动3s时,P点停止运动,Q点以原速立即向B点返回,在返回的过程中,DP是否能平分∠ADQ?若能,求出点Q运动的时间;若不能,请说明理由.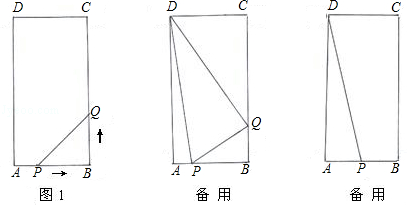
如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
(1)DE与AB的长度之比是多少?
(2)已知直角三角形ABC的周长是12cm,面积是6cm2,求直角三角形DEF的周长与面积.