已知：在如图1所示的平面直角坐标系xOy中，A，C两点的坐标分别为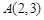
，
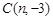（其中n＞0），点B在x轴的正半轴上．动点P从点O出发，在四边形OABC的边上依次沿O—A—B—C的顺序向点C移动，当点P与点C重合时停止运动．设点P移动的路径的长为l，△POC的面积为S，S与l的函数关系的图象如图2所示，其中四边形ODEF是等腰梯形．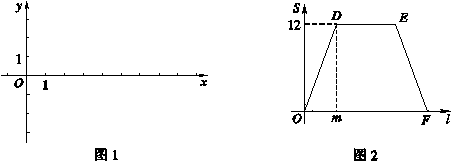
（1）结合以上信息及图2填空：图2中的m= ；
（2）求B，C两点的坐标及
图2中OF的长；（3）在图1中，当动点P恰为经过O，B两点的抛物线W的顶点时，
① 求此抛物线W的解析式；
② 若点Q在直线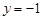
上方的抛物线W上，坐标平面内另有一点R，满足以B，
P，Q，R四点为顶点的四边形是菱形，求点Q的坐标．
，
被直线
所截，在括号内为下面各小题的推理填上适当的根据.