如图,在区域I(0≤x≤d)和区域II(d≤x≤2d)内分别存在匀强磁场,磁感应强度大小分别为B和2B,方向相反,且都垂直于Oxy平面。一质量为m、带电荷量q(q>0)的粒子a于某时刻从y轴上的P点射入区域I,其速度方向沿x轴正向。已知a在离开区域I时,速度方向与x轴正方向的夹角为30°;此时,另一质量和电荷量均与a相同的粒子b也从p点沿x轴正向射入区域I,其速度大小是a的1/3。不计重力和两粒子之间的相互作用力。求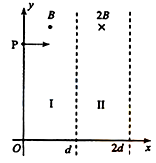
粒子a射入区域I时速度的大小;
当a离开区域II时,a、b两粒子的y坐标之差。
消防队员为缩短下楼时间,往往抱着一根竖直杆直接滑下.假设一名质量为60 kg的消防队员从离地面18 m的高度抱着竖直的杆先做自由落体运动,下降7.2m后立即抱紧直杆,做匀减速下滑,抱紧直杆时,手和腿对杆的压力为1800 N,手和腿与杆之间的动摩擦因数为0.5,设当地的重力加速度 g=10 m/s2.假设杆是固定在地面上的,杆在水平方向不移动.试求:
(1)消防队员下滑过程中的最大速度
(2)消防队员下滑过程中受到的滑动摩擦力
(3)消防队员着地时的速度
如图所示,木块的质量m =" 2" kg,与地面间的动摩擦因数μ= 0.2,木块在拉力F=10N作用下,在水平地面上向右做匀加速直线运动,经3s时间撤去外力F.已知力F与水平方向的夹角θ= 37°,sinθ=0.6,cosθ=0.8,g 取 10 m/s2.试问:
(1)撤去外力前,物体运动的加速度大小
(2)刚撤去外力时,物体运动的速度
(3)撤去外力后,到停止滑行的距离
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37º足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的速度—时间图线,如图所示(取sin37º=0.6 cos37º=0.8
g =10m/s2)求:
(1)小物块冲上斜面过程中加速度的大小
(2)小物块与斜面间的动摩擦因数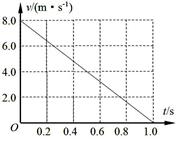
用三根轻绳将质量为m的物块悬挂在空中,如图,已知ac和bc与水平方向的夹角分别为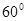 和
和 ,则ac绳和bc绳中的拉力分别是多少?
,则ac绳和bc绳中的拉力分别是多少?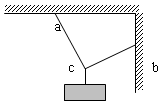
如图,在光滑的水平面上有一辆很长的小车以速度v向右运动,小车的质量为M ,前方很远的地方有一与车等高的竖直光滑半径为R的半圆,直径AB在竖直方向上。现在有一个质量为m的滑块以同样的速度为v冲上小车,已知车的质量大于滑块的质量,滑块与车之间的动摩擦因数为μ。求:
(1)滑块的最终速度;
(2)滑块向左运动的最远距离;
(3)如果滑块冲上小车的瞬间,车与B的距离为 ,且M=3m,M与B处碰后立即停下,滑块能否通过A点?若能,求出滑块落点到B的距离。
,且M=3m,M与B处碰后立即停下,滑块能否通过A点?若能,求出滑块落点到B的距离。