为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度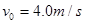 ,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数
,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数 (g取10m/s2,
(g取10m/s2, 0,
0, )求:
)求:小物块的抛出点和A点的高度差;
为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件。
要使小物块不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件.

如图,在高为h=5 m的平台右边缘上,放着一个质量M=3 kg的铁块,现有一质量为m=1 kg的钢球以v0=10 m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为L=2 m,已知铁块与平台之间的动摩擦因数为0.5 (不计空气阻力,铁块和钢球都看成质点,取g=10 m/s2) ,求: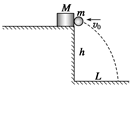
(1)钢球碰后反弹的速度;(2)铁块在平台上滑行的距离s。
有一玻璃半球,右侧面镀银,光源S就在其对称轴SO上(O为球心),且SO水平,如下图所示。从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折入玻璃半球内,经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R,玻璃折射率为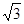 ,求光源S与球心O之间的距离SO为多大?
,求光源S与球心O之间的距离SO为多大?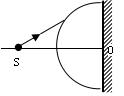
一定质量的理想气体从状态A变化到状态B再变化到状态C,其状态变化过程的P-V图象如图所示。已知该气体在状态A时的温度为27℃。求: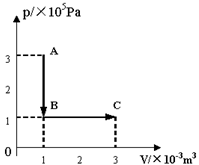
①该气体在状态B、C时的温度各为多少℃;
②该气体从状态A到状态C的过程中是吸热还是放热?传递的热量是多少.
如图所示,在xOy坐标系中,两平行金属板AB、OD如图甲放置,OD与x轴重合,板的左端与原点O重合,板长L=2 m,板间距离d=1 m,紧靠极板右侧有一荧光屏.两金属板间电压UAO随时间的变化规律如图乙所示,变化周期为T=2×10-3 s,U0=103 V,t=0时刻一带正电的粒子从左上角A点,以平行于AB边v0=103 m/s的速度射入板间,粒子带电荷量为q=10-5 C,质量m=10-7 kg.不计粒子所受重力.求: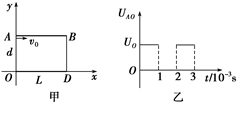
(1)粒子在板间运动的时间;
(2)粒子打到荧光屏上的纵坐标;
(3)粒子打到荧光屏上的动能.
如图(甲)所示,质量m="2" kg的物体在水平面上向右做直线运动。过P点时给物体作用一个水平向左的恒力F并开始计时,选取水平向右为速度的正方向,通过速度传感器测出物体的瞬时速度,所得v t图像如图(乙)所示。取重力加速度为g="10" m/s2。求:
t图像如图(乙)所示。取重力加速度为g="10" m/s2。求: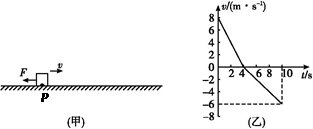
(1)物体在0~4 s内和4~10 s内的加速度a1、a2的大小;
(2)力F的大小和物体与水平面间的动摩擦因数μ;
(3)10 s末物体离P点的距离。