如图所示,一根长为三的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和mb,,杆可绕距a球为L/4处的水平定轴D在竖直平面内转动,初始时杆处于竖直位置,小球b几乎接触桌面,在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面.现用一水平恒力F作用于a球上,使之绕O轴逆时针转动,设在此过程中立方体物块没有发生转动,且小球b立方体物块始终接触没有分离.不计一切摩擦,求:
在细杆转动过程中a、b两小球速度大小的关系.
当细杆转过口角时小球6速度大小与立方体物块速度大小的关系.
若ma=3mb=m,当细杆转过30°角时小球b速度的大小.
如右图所示的电路中,电源电动势E=6.0V,内阻r=0.6Ω,电阻R2=0.5Ω,当开关S断开时;电流表的示数为1.5A,电压表的示数为3.0V,试求:
(1)电阻R1和R3的阻值;
(2)当S闭合后,电压表的示数、以及R2上消耗的电功率。
如图,甲、乙两运动员在训练接力赛的交接棒。已知甲、乙两运动员经短距离加速后都能达到并保持8m/s的速度跑完全程。设乙从起跑后到接棒前的运动是匀加速的,加速度大小为2.5m/s2. 乙在接力区前端听到口令时起跑,在甲乙相遇时完成交接棒.在某次练习中,甲以v=8m/s的速度跑到接力区前端s0=11.0m处向乙发出起跑口令.已知接力区的长度为L=20m.求:
(1)此次练习中交接棒处离接力区前端的距离.
(2)为了达到理想成绩,需要乙恰好在速度达到与甲相同时被甲追上,则甲应在接力区前端多远时对乙发出起跑口令?
(3)在(2)中,棒经过接力区的时间是多少?
在某路段相邻较近的两红绿灯路口之间,一辆汽车在第一个路口从静止开始以5m/s2的加速度做匀加速运动,在行驶过40m时立即以1.25 m/s2做匀减速直线运动,正好在到达下一个路口时停止运动,求:
(1)汽车从启动到停止所用的时间;
(2)两红绿灯路口间的距离.
如图所示,重300 N的物体放在水平地面上,已知物体与水平地面间的最大静摩擦力为152 N,动摩擦因数是0.5,物体的一端连一根劲度系数为5×103 N/m的轻质弹簧.试问:
(1)将弹簧拉长2cm时,物体受到地面的摩擦力多大?
(2)将弹簧拉长4cm时,物体受到地面的摩擦力多大?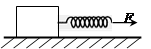
2012年10月14日极限运动员鲍姆加特纳从距地面高度约3.9万米的氦气球携带的太空舱上跳下并成功着陆,在打开降落伞之前飞行速度最高达到373m/s,成为首位超音速自由落体的跳伞运动员.由于3.9万米高空处于平流层,空气阻力影响可忽略,经过35s他下落的速度就达到了音速340m/s,求:
(1)平流层处的重力加速度;
(2)35s内下落的高度.