如图所示，真空有一个半径r=0．5 m的圆形磁场，与坐标原点相切,磁场的磁感应强度大小B=2×10-3 T,方向垂直于纸面向里，在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0．5 m的匀强电场区域，电场强度E=1．5×103 N/C。在x="2" m处有一垂直x方向的足够长的荧光屏，从O点处向不同方向发射出速率相同的荷质比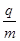
=1×109 C/kg带正电的粒子，粒子的运动轨迹在纸面内，一个速度方向沿y轴正方向射入磁场的粒子，恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求：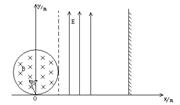
粒子进入电场时的速度和沿y轴正方向射入的粒子在磁场中运动的时间？
速度方向与y轴正方向成30°（如图中所示）射入磁场的粒子，离开磁场时距x轴的距离是多大？求最后打到荧光屏上，求该发光点的位置坐标。
电荷量为q=1×10－4C的带正电小物块置于粗糙的绝缘水平面上，所在空间存在沿水平方向的匀强电场，场强E与时间t的关系及物块速度v与时间t的关系如图所示。若重力加速度g取10 m/s2，求：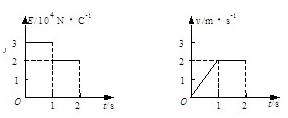
（1）物块的质量m。
（2）物块与水平面之间的动摩擦因数。
（3）物块运动2s过程中，其电势能的改变量。
如图所示，小球A和B带电荷量均为+q，质量分别为m和2m，用不计质量的竖直细绳连接，在竖直向上的匀强电场中以速度v0匀速上升，某时刻细绳突然断开。小球A和B之间的相互作用力忽略不计。求：
（1）该匀强电场的场强E
（2）细绳断开后A、B两球的加速度aA、aB
（3）当B球速度为零时，A球的速度大小
如图所示，倾角为30°的直角三角形底边长为2 L，底边处在水平位置，斜边为光滑绝缘导轨，现在底边中点O处固定一正电荷Q，让一个质量为m的带正电质点q从斜面顶端A沿斜边滑下（不脱离斜面），已知它滑到斜边上的D点（BD⊥AC）时加速度为a，方向沿斜面向下，求该质点刚要滑到斜边底端C点时的加速度。
如图所示，在光滑绝缘水平面上固定质量相等的三个带电小球(可视为点电荷)a、b、c，三球共线.若释放a球，其初始加速度为1m/s2,方向向左；若释放c球，其初始加速度为3m/s2，方向向右；若释放b球，则b球的初始加速度的大小是多少?方向如何?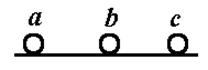
在真空中有一个点电荷，受到距它1.0cm处的另一个点电荷的吸引，引力大小为2.7×10-5N.已知其中一个点电荷的电量是3.0×10-9C，那么另一点电荷的电量是C.