如图,已知A(n,-2),B(1,4)是一次函数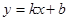 的图象和反比例函数y=
的图象和反比例函数y=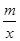 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.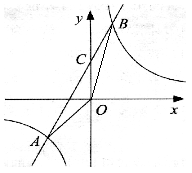
(1)求反比例函数和一次函数的关系式;
(2)求△AOB的面积;
(3)求不等式
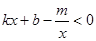 的解集(直接写出答案).
的解集(直接写出答案).
如图,在△ABC中;
(1)作∠C的角平分线CE交AB于E(保留痕迹,不写作法),过点E分别作AC、BC的垂线EM、EN,垂足分别为M、N;
(2)若EN=2,AC=4,求△ACE的面积.
画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
某学校为丰富课间自由活动的内容,随机选取本校100名学生进行调查,调查内容是“你最喜欢的自由活动项目是什么”,整理收集到的数据,绘制成直方图,如图.
(1)喜欢“踢毽子”的学生有 _________ 人,并在图中将“踢毽子”部分的条形图补充完整;
(2)喜欢“跳绳”的频率是 _________ ;
(3)该校共有800名学生,估计喜欢“跳绳”的学生有 _________ 人.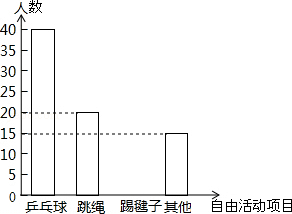
如图,在▱ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.
(1)从对称性质看,▱ABCD是 _________ 对称图形;
(2)求平行四边形ABCD的周长.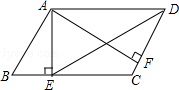
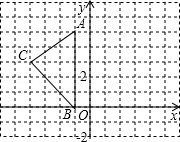
如图,在平面直角坐标系中,已知A(﹣1,5),B(﹣1,0),C(﹣4,3).
①在图中作出△ABC关于y轴的对称图形△A1B1C1;
②写出点A1和C1的坐标.