(文)正数列 的前
的前 项和
项和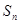 满足:
满足: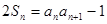 ,
,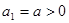
(1)求证: 是一个定值;
是一个定值;
(2)若数列 是一个单调递增数列,求
是一个单调递增数列,求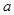 的取值范围;
的取值范围;
(3)若 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数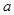 .
.
已知:A、B、C是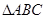 的内角,
的内角,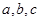 分别是其对边长,向量
分别是其对边长,向量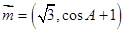 ,
,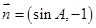 ,
,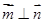 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若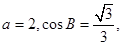 求
求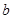 的长.
的长.
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=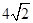 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。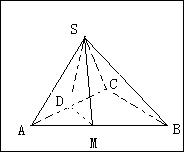
已知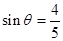 ,
,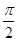 <θ<π.
<θ<π.
(1) 求tanθ;
(2)求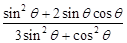 的值.
的值.
某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
设函数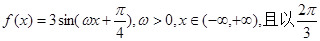 为最小正周期.
为最小正周期.
(1)求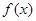 的解析式;
的解析式;
(2)已知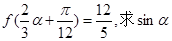 的值.
的值.