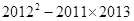已知:抛物线 与x轴交于
与x轴交于
点A(x1,0)、B(x2,0),且x1<1<x2.求A、B两点的坐标(用a表示);
设抛物线的顶点为C,求△ABC的面积;
若a是整数,P为线段AB上的一个动点(P点与A、B两点不重合),
在x轴上方作等边△APM和等边△BPN,记线段MN的中点为Q,求抛物线的
解析式及线段PQ的长的取值范围.
如图,居民楼与马路是平行的,相距9m,在距离载重汽车41m处就可受到噪声影响,试求在马路上以4m/s速度行驶的载重汽车,给一楼的居民带来多长时间的噪音影响?若时间超过25秒,则此路禁止该车通行,你认为载重汽车可以在这条路上通行吗? 
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点就做格点,以格点为顶点分别按下列要求画三角形;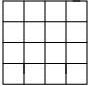
①使三角形的三边长分别为1,3,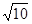 (在图①中画出一个既可);
(在图①中画出一个既可);
②使三角形为钝角三角形且面积为3(在图②中画出一个既可),并计算你所画三角形的三边的长。
把下列各式因式分解:
(1)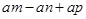 (2)
(2)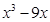
(3)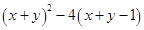 (4)
(4)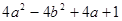
先化简,后求值:(2x-1)2-(3x+1)(3x-1)+5(x+5)(x-1),其中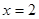 .
.
计算:(1)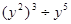 (2)
(2)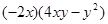
(3)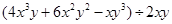 (4)
(4)