如图所示，地面和半圆轨道面均光滑。质量M=1kg、长L=4m的小车放在地面上，其右端与墙壁距离为S，小车上表面与半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块（不计大小）以v0=6m/s的初速度滑上小车左端，带动小车向右运动。小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数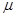
=0.2，g取m/s2。求小车与墙壁碰撞时的速度；
要滑块能沿圆轨道运动而不脱离圆轨道，求半圆轨道的半径R的取值。
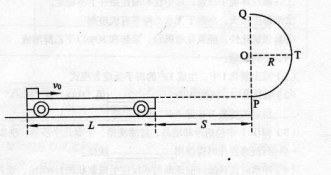
两个氘核发生了如下核反应：
，其中氘核质量为2.1036u，氢核质量为3.1050u，中子质量为1.0087u。求：
①核反应中释放的核能。
②在两个氘核以相等的动能0.35MeV进行对心碰撞，并且核能全部转化为机械能的情况下，求反应中产生的中子和氦核的动能。
③假设反应中产生的氦核沿直线向原来静止的碳核(
C)接近，受库仑力的影响，当它
们的距离最近时，两个原子核的
动能各是多少?
氢原子在某三个相邻能级之间跃迁时，可能发出三种不同波长的辐
射光。已知其中的两个波长分别为
和
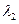，且>。
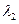求：另一个波长可能是多少？
某物理兴趣小组想测量太阳辐射的功率，其做法是取一个横截面积是3×10—2m2的不高的圆筒，筒内装满0.6kg的水。某天中午在太阳光的照射下，测得2分钟后水温升高了1℃ 。该小组同学已经查的资料有下列一些：
| R地=6400km |
M地=5.97×1024kg |
Q=CmΔt |
射到地球大气层顶层的太阳能只有43℅达到地面，另外57℅被大气吸收或反射而未到达地面 |
| R日地=1.5×108km |
太阳质量：1.9891×1030kg |
ΔU=W+Q |
|
| 水的密度: 1.0×103kg/m3 |
水的比热： 4.2×103J/(kg.℃) |
球的表面积： S=4πr2 |
根据上述资料和实验数据计算：
（1）在阳光直射下，地球
表面每平方厘米的面积上每分钟获得的能量
（2）估算太阳辐射的功率（保留两位有效数字）
U形均匀玻璃管，左端开口处有一重力可不计的活塞，右端封闭，在大气压强p0＝75cmHg、气温t0＝87℃时，管内汞柱及空气柱长度(单位cm)如图所示，活塞的截面积为5.0×10-5m2，lcmHg＝1.33×103Pa.试求：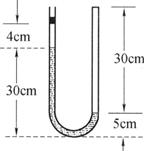
(1)若使气体温度下降到t1＝－3℃，活塞将移动的距离.
(2)保持气体温度t1＝－3℃不变，用细杆向下推活塞，至管内两边汞柱高度相等，此时细杆对活塞的推力大小.
容积为2L的烧瓶，在压强为1.0×105Pa时，用塞子塞住，此时温度为27℃，当把它加热到127℃时，塞子被顶开了，稍过一会儿，重新把塞子塞好，停止加热并使它逐渐降温到27℃，求：(1)塞子被顶开前的最大压强；(2)27℃时剩余空气的压强．