某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如下表所示:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
| 物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
| 物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
某数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀.
有多少的把握认为学生的数学成绩与物理成绩之间有关系( )
A. 99.9%
B. 99%
C. 97.5%
D. 95%
下列不等式中成立的是()
A.若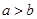 ,则 ,则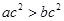 |
B.若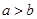 ,则 ,则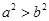 |
C.若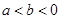 ,则 ,则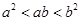 |
D.若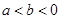 ,则 ,则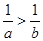 |
在平面直角坐标系内,设 、
、 为不同的两点,直线
为不同的两点,直线 的方程为
的方程为 ,
,  .有四个判断:
.有四个判断:
①若 ,则过
,则过 、
、 两点的直线与直线
两点的直线与直线 平行;
平行;
②若 ,则直线
,则直线 经过线段
经过线段 的中点;
的中点;
③存在实数 ,使点
,使点 在直线
在直线 上;
上;
④若 ,则点
,则点 、
、 在直线
在直线 的同侧,且直线
的同侧,且直线 与线段
与线段 的延长线相交.
的延长线相交.
上述判断中,正确的是()
| A.①②③ | B.①②④ | C.①③④ | D.①②③④ |
函数 ,其中
,其中 ,若动直线
,若动直线 与函数
与函数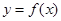 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为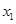 、
、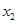 、
、 ,则
,则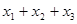 的取值范围是()
的取值范围是()
A.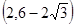 |
B.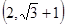 |
C.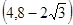 |
D. |
已知函数 是定义在
是定义在 上的奇函数,若对于任意给定的不等实数
上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式 恒成立,则不等式
恒成立,则不等式 的解集为()
的解集为()
A. |
B. |
C. |
D. |
已知三个互不重合的平面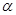 ,
,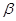 ,
, ,且
,且 ,
,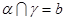 ,
, ,给出下列命题:①
,给出下列命题:① ,
,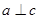 ,则
,则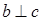 ;
;
②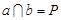 ,则
,则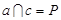 ;
;
③若 ,
,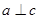 ,则
,则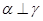 ;
;
④若 ,则
,则 。
。
其中正确命题的个数为()
| A.1 | B.2 | C.3 | D.4 |