如图所示装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接,其中轨道AB、CD段是光滑的,水平轨道BC的长度s=5m,轨道CD足够长且倾角θ=370,A、D两点离轨道BC的高度分别为h1="4.30" m、h2="l.35" m.现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数μ=0.5,重力加速度g取10m/s2,sin370=0.6、cos370=0.8.求:
小滑块第一次到达D点时的速度大小;
小滑块第一次与第二次通过C点的时间间隔.
屋檐上每间隔一定时间滴出一滴水,当第5滴水滴正欲滴下时,第1滴刚好到达地面,而第3滴与第2滴水滴正分别位于高1m的窗户的上、下沿,(如图所示,取g = 10m/s2),试求:
(1)相临两滴水的时间间隔;
(2)此时第2滴水距离地面的高度.
观光电梯由静止开始先做匀加速上升,经过5s速度达到4m/s,接着匀速上升20s,然后以大小为1 m/s2的加速度做匀减速运动,并恰好停在最顶层,求:
(1)加速上升时的加速度大小;
(2)从开始减速到停止所需时间;
(3)整个过程中,电梯上升的总高度.
电动机通过一条绳子吊起质量为8kg的物体。绳的拉力不能超过120N,电动机的功率不能超过1200W,要将此物体由静止起,用最快的方式将物体吊高90m(已知物体在被吊高90m以前已开始以最大速度匀速上升),所需时间为多少?(g取10 m/s2)
.如图所示,长为L的绝缘细线一端悬于O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。求: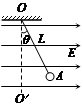
(1)该匀强电场的电场强度大小;
(2)若将小球求从O′点由静止释放,则小球运动到A点时的速度υ多大?
质量为0.2kg的物体,以24m/s的初速度竖直向上抛出,由于空气的阻力,经2s到达最高点。假设物体在运动过程中所受的空气阻力大小不变,求:(1)物体上升的最大高度;(2)物体由最高点落回抛出点所用的时间。(g取10m/s2)