如图所示,把质量为m、带电量为+Q的物块放在倾角α=60°的固定光滑绝缘斜面的顶端,整个装置处在范围足够大的匀强电场中。已知电场强度大小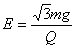 ,电场方向水平向左,斜面高为H,则释放物块后,物块落地时的速度大小为
,电场方向水平向左,斜面高为H,则释放物块后,物块落地时的速度大小为
A. |
B.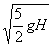 |
C. |
D.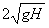 |
在下面所说物体运动情况中,说法错误的是:
| A.物体在某一时刻运动速度很大,并且加速度很大 |
| B.物体在某一时刻运动速度很小,而加速度很大 |
| C.物体在某一时刻速度为零,而其加速度不为零 |
| D.物体在拐弯时, 若其速度方向改变但大小不变,则物体的运动状态不发生变化 |
关于伽俐略对自由落体运动的研究,下列哪个过程是他的探究过程:
| A.猜想——问题——数学推理——实验验证——合理外推——得出结论 |
| B.问题——猜想——实验验证——数学推理——合理外推——得出结论 |
| C.问题——猜想——数学推理——实验验证——合理外推——得出结论 |
| D.猜想——问题——实验验证——数学推理——合理外推——得出结论 |
某质点的位移随时间变化的关系式为 ,s与 t的单位分别是 m和s,则质点的 :
,s与 t的单位分别是 m和s,则质点的 :
| A.初速度为3m/s | B.初速度为5m/s |
| C.加速度为6m/s2 | D.加速度为3m/s2 |
下列所说速度中是瞬时速度的有:
| A.百米赛跑中,8s末的速度为12.5m/s | B.百米赛跑中,50 m处的速度为10 m/s |
| C.汽车在一百米内的速度为8 m/s | D.子弹出枪口的速度为800 m/s |
关于位移和路程,以下说法正确的是:
| A.在直线运动中,位移大小一定与路程相同 |
| B.上学时从家到学校,放学时从学校到家,这两次的位移是相同的 |
| C.位移是矢量,路程是标量 |
| D.当运动物体的始末位置确定以后,位移就唯一确定了,而路程可以有多个 |