小亮妈妈下岗后开了一家糕点店.现有10.2千克面粉.10.2千克鸡蛋.计划加工一般糕点和精制糕点两种产品共50盒.已知加工一盒一般糕点需0.3千克面粉和0.1千克鸡蛋;加工一盒精制糕点需0.1千克面粉和0.3千克鸡蛋.
(1)有哪几种符合题意的加 工方案?请你帮助设计出来;
工方案?请你帮助设计出来;
(2)若销售一盒一般糕点和一盒精制糕点的利润分别为1.5元和2元.那么按哪一个方案加工.小亮妈妈可获得最大利润?最大利润是多少?
济南与北京两地相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度是普通快车的3倍,求高铁列车的平均行驶速度.
(1)化简:(x+2)2+x(x+3)
(2)解不等式组: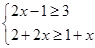 .
.
某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件。
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
解不等式组: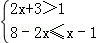 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.