下列四个数中最小的是
A． |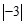
B． |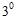
C． |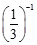
D． |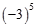
如图，在△ABC中，∠C＝90°，BC＝6，D，E分别在AB，AC上，将△ADE沿DE翻折后，点A落在点A'处，若A'为CE的中点，则折痕DE的长为（）
| A．1 | B．2 | C．4 | D．6 |
计算
的值为（）
| A．0 | B．25 | C．50 | D．80 |
如图，矩形AOBC中，顶点C的坐标（4，2），又反比例函数y＝
的图像经过矩形的对角线的交点P，则该反比例函数关系式是（）
A．y＝ （x＞0） |
B．y＝ （x＞0） |
C．y＝ （x＞0） |
D．y＝ （x＞0） |
如图，点F是□ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（）
A． |
B． |
C． |
D． |