、(8分)已知一次函数y=Kx+b的图象过点(3,5)与(-4,-9),(1)求这个一次函数解析式。
(2)利用函数图象求当x为何值时,y>0。
已知:二次函数y=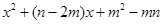 .
.求证:此二次函数与x轴有交点;
若m-1=0,求证方程
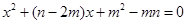 有一个实数根为1;
有一个实数根为1;在(2)的条件下,设方程
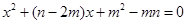 的另一根为a,当x=2时,关于n 的函数
的另一根为a,当x=2时,关于n 的函数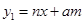 与
与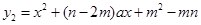 的图象交于点A、B(点A在点B的左侧),平行于y轴的直线L与
的图象交于点A、B(点A在点B的左侧),平行于y轴的直线L与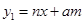 、
、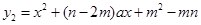 的图象分别交于点C、D,若CD=6,求点C、D的坐标.
的图象分别交于点C、D,若CD=6,求点C、D的坐标.
已知菱形纸片ABCD的边长为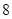 ,∠A=60°,E为
,∠A=60°,E为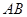 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点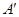 处,过点
处,过点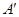 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点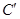 处,
处,  与
与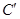 H分别交
H分别交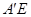 与
与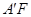 于点M、N.若点
于点M、N.若点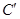 在△
在△ EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.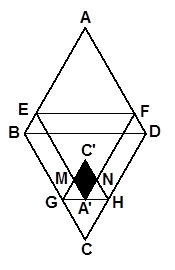

若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形
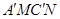 的面积;
的面积;实验探究:设AE的长为
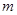 ,若重叠四边形
,若重叠四边形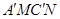 存在.试用含
存在.试用含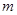 的代数式表示重叠四边形
的代数式表示重叠四边形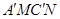 的面积,并写出
的面积,并写出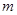 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
已知:如图,在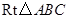 中,
中,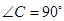 ,点
,点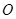 在
在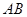 上,以
上,以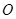 为圆心,
为圆心, 长为半径的圆与
长为半径的圆与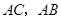 分别交于点
分别交于点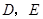 ,且
,且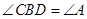 .
.
判断直线
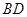 与
与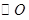 的位置关系,并证明你的结论;
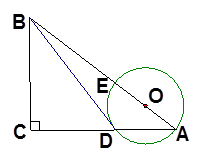
的位置关系,并证明你的结论;若
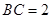 ,
,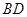 =
=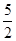 ,求
,求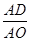 的值
的值
在△ABC中,AB=AC,∠BAC=120°,过点C作CD∥AB,且CD=2AB,联结BD,BD=2.求△ABC的面积.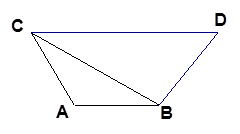
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)求反比例函数与二次函数的解析式;
设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积