（本题8分）数学课上，老师出示了如下框中的题目．
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况•探索结论
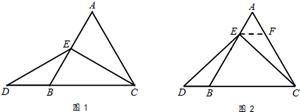
当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：
AE DB（填“＞”，“＜”或“=”）．
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE DB（填 “＞”，“＜”或“=”）．
理由如下：如图2，过点E作EF∥BC，交AC于点F.（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的
边长为1，AE=2，求CD的长（请你直接写出结果） ．
 |
如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测得∠DAN=35°，然后沿河岸走了120米到达B处，测得∠CBN=70°.求河流的宽度CE.(结果保留两个有效数字)（参考数据：sin35°≈0.57,cos35°≈0.82,tan35°≈0.70， Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)[来源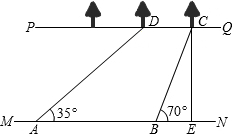
如图，在梯形ABCD中，AD∥BC,BD平分∠ABC，AE∥CD交BC于E,求证：AB=EC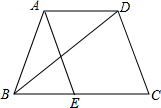
解方程：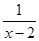
=
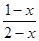－3
如图1，抛物线
经过A（-1，0），C（3，-2）两点，与
轴交于点D，与
轴交于另一点B．
（1）求此抛物线的解析式；
（2）若直线
（
）将四边形ABCD面积二等分，求
的值；
（3）如图2，过点E（1，1）作EF⊥轴于点F，将△AEF绕平面内某点P旋转180°得△MNQ（点M、N、Q分别与点A、E、F对应），使点M、N在抛物线上，求点N和点P的坐标？
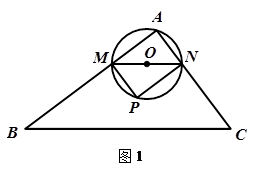
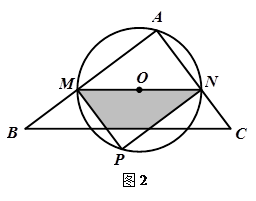
在△ABC中，∠A=90°，AB=8，AC=6，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．
设AM=x．
（1）用含x的代数式表示△MNP的面积S；
（2）在动点M的运动过程中，记△MNP与梯形BCNM重合部分的面积为y，试求关于y的函数表达式，并求 x为何值时，y的值最大，最大值是多少？
