(本题满分12分)某电视生产厂家今年推出A、B、C、D四种款式电视机,每种款式电视机的外观均有黑色、银白色两种。四月份的电视机产量如下表(单位:台)
| |
款式A |
款式B |
款式C |
款式D |
| 黑色 |
150 |
200 |
200 |
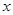 |
| 银白色 |
160 |
180 |
200 |
150 |
若按电视机的款式采取分层抽样的方法在这个月生产的电视机中抽取70台,其中有C种款式的电视机20台。
(1) 求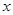 的值;
的值;
(2) 若在C款式电视机中按颜色进行分层抽样抽取一个容量为6的样本,然后将该样本看成一个总体,从中任取2台,求恰有1台黑色、1台银白色电视的概率;
(3) 用简单随机抽样的方法从A种款式电视机中抽取10台,对其进行检测,它们的得分如下:94,92,92,96,97,95,98,90,94,97。如果把这10台电视机的得分看作一个样本,从中任取一个数,求该数与样本平均数之差的绝对值不超过2的概率。
已知函数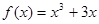
(1)求该函数的导函数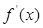 ;
;
(2)求曲线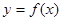 在点
在点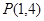 处的切线方程.
处的切线方程.
如图:已知三棱锥 中,
中, 面
面 ,
, ,
, ,
, 为
为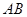 上一点,
上一点,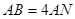 ,
, 分别为
分别为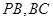 的中点.
的中点.
(1)证明: .
.
(2)求面 与面
与面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(3)在线段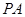 (包括端点)上是否存在一点
(包括端点)上是否存在一点 ,使
,使 平面
平面 ?若存在,确定
?若存在,确定 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.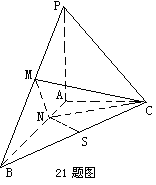
若抛物线的顶点是双曲线 的中心,焦点是双曲线的右顶点.
的中心,焦点是双曲线的右顶点.
(1)求抛物线的标准方程.
(2)若直线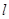 过点
过点 交抛物线于
交抛物线于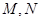 两点,是否存在直线
两点,是否存在直线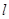 ,使得
,使得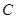 恰为弦
恰为弦 的中点?若存在,求出直线
的中点?若存在,求出直线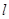 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
如右图,一个结晶体的形状为平行六面体,以点 为端点的三条棱
为端点的三条棱
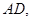
 的长都等于
的长都等于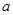 ,且彼此之间的夹角都是
,且彼此之间的夹角都是 .
.
(1)用向量
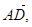
 表示向量
表示向量 .
.
(2)求晶体的对角线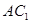 长.
长.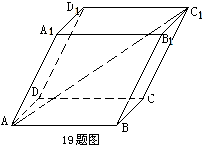
已知抛物线的顶点为椭圆
 的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点
的中心,椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.