(本题满分12分)在平面直角坐标系中,抛物线交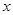 轴于
轴于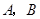 两点,交
两点,交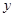 轴于点
轴于点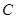 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 .
.
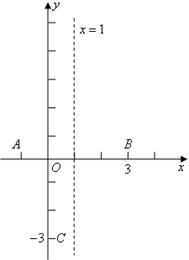 |
⑴求这个抛物线的解析式;
⑵在抛物线的对称轴上是否存在一点
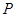 ,使点
,使点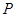 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点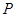 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(3)如果在
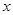 轴上方平行于
轴上方平行于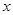 轴的一条直线交抛物线于
轴的一条直线交抛物线于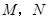 两点,以
两点,以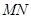 为直径作圆恰好与
为直径作圆恰好与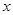 轴相切,求此圆的直径.
轴相切,求此圆的直径.
利用图11.1、图11.2提供的信息,回答下列问题:
(1)某企业2009年管理费支出的金额是万元,保险费用支出的金额是万元;
(2)原料占2009年总支出额的百分比为,这个扇形的圆心角的度数为°;
(3)2009年总支出比2008年增加万元,增加百分比为 (精确到0.1%).
一种商品每件成本a元,按成本增加22%定出价格,后来因库存积压减价,按原价的85%出售. 试用含a的代数式表示.
(1)该商品最初每件的定价为多少元?
(2)该商品每件按定价的85%出售后,售价为多少元?每件还能盈利多少元?
2(2xy2- y2)-(4xy2+
y2)-(4xy2+ y2-x2y)-
y2-x2y)- y2,其中x=
y2,其中x= ,y=-
,y=-
(1) ;
;
(2) .
.
如图11,正方形ABCD的边长为5,点F为正方形ABCD内的点,△BFC经逆时针旋转后能与△BEA重合.
(1)旋转中心是哪一点?旋转了多少度?
(2)判断△BEF是怎样的三角形?并说明理由;
(3)若BE=3,FC=4,说明AE∥BF.