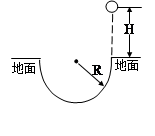
如图所示,质量为m =0.5kg的小球从距离地面高H=5m处自由下落,到达地面时恰能沿凹陷于地面的半圆形槽壁运动,半圆形槽的半径R为0.4m,小球到达槽最低点时速率恰好为10m/s,并继续沿槽壁运动直到从槽左端边缘飞出且沿竖直方向上升、下落,如此反复几次,设摩擦力大小恒定不变。
求:(1)小球第一次飞出半圆槽上升距水平地面的高度h为多少?
(2)小球最多能飞出槽外几次?(g=10m/s2)。
 |
2011年8月10日,我国首艘航空母舰“瓦良格”号出海试航。该航母上跑道长300m,某种飞机的起飞速度为60m/s。
(1)要使该种飞机能够在跑道上由静止开始匀加速滑行后起飞,飞机的加速度至少要多大?
(2)若该飞机刚好能在跑道上由静止开始匀加速滑行起飞,飞机在跑道上滑行的时间为多少?
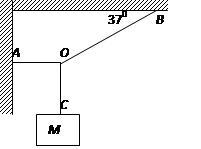
(6分)如图所示,质量为M=6kg的物体处于静止状态,细绳OB与水平方向夹角为37°,细绳OA沿水平方向。求:OA、OB两根细绳的拉力大小。(取g =" 10" m/s2,sin37°=0.6,cos37°=0.8)
 |
质量为5kg的木块放在水平木板上,木块与木板间的动摩擦因数为0.75,要使木块能沿木板匀速滑动,需给木块施加水平力为F,请画出木块在木板上匀速运动时的受力分析图,并求出力F的大小是多少?(g=10m/s2)
以10m/s的速度行驶的列车开始下坡,在坡路上做匀加速直线运动的加速度等于0.2m/s2,经来30s到达坡底,求:⑴列车到达坡底时的速度;⑵坡路的长度
如图所示,质量为m的小球通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,开始时系统处于静止状态。
(1)求系统静止时,绳对小球的拉力大小和斜面对小球的支持力大小。
(2)当系统以多大的加速度向左运动时,斜面对小球的支持力恰好为零?