设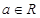
，函数
的导函数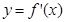
是奇函数，若曲线
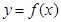的一条切线斜率为
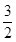，则切点的横坐标为（ ）
A． |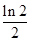
B． |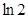
C． |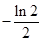
D． |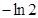
极坐标方程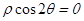
表示的曲线为（）
| A．极点 | B．极轴 | C．一条直线 | D．两条相交直线 |
将函数
的图像上各点的横坐标伸长到原来的2倍（纵坐标不变），再向左平移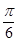
个单位，所得函数图像的一条对称轴为（）
A． |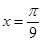
B． |
C． |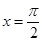
D． |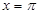
如图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60º，O为球心，则直线OA与截面ABC所成的角是（）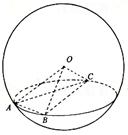
A．arcsin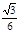
B．arccos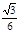C．arcsin
D．arccos
已知
展开式中常数项为1120，其中实数a是常数，则展开式中各项系数的和是（）
| A．28 | B．38 | C．1或38 | D．1或28 |
已知a、b是非零向量且满足(a－2b) ⊥a，(b－2a) ⊥b，则a与b的夹角是（）
A． |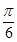
B． |
C． |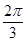
D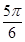． |