某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日到3日的每天昼夜温差与实验室每天每100颗种子发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
| 温差x(0C) |
11 |
13 |
12 |
| 发芽数y(颗) |
25 |
30 |
26 |
该农科所确定的研究方案是:先从这3组数据求出线性回归方程,再对12月4日的数据进行推测和检验.则根据以上3天的数据,求出y关于x的线性回归方程是
A.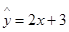 
B. 
C. 
D.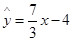 
等比数列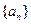
的各项均为正数，且
则
（）
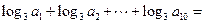| A．12 | B．10 | C．8 | D． |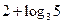
把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的
是较小的两份之和，则最小1份是（）
A． |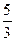
B． |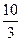
C． |
D． |
在长方体ABCD—A1B1C1D1中，过A1，C1，B作一截面，则截得的棱锥的体积占剩下的几何体体积的比是（）
A． |
B． |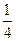
C． |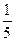
D． |
下列命题中，正确的个数是（）
①垂直于同一直线的两个平面互相平行；②垂直于同一平面的两条直线互相平行
③平行于同一直线的两个平面互相平行；④平行于同一平面的两条直线互相平行
| A．1 | B．2 | C．3 | D．4 |
三个平面可将空间分成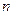
个部分，则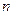的最小最大值分别是（）
| A．4，7 | B．6，7 | C．4，8 | D．6，8 |