据报道，最近已研制出一种可以投入使用的电磁轨道炮，其原理如右图所示．炮弹(可视为长方形导体)置于两固定的平行导轨之间，并与轨道壁密接．开始时炮弹在导轨的一端，通电流后，炮弹会被磁场力加速，最后从位于导轨另一端的出口高速射出．设两导轨之间的距离d＝0.10m，导轨长L＝5.0m，炮弹质量m＝0.30kg.导轨上的电流I的方向如图中箭头所示．可认为，炮弹在轨道内运动时，它所在处磁场的磁感应强度始终为B＝2.0T，方向垂直于纸面向里．若炮弹出口速度为υ＝2.0×103m/s，求通过导轨的电流I．(忽略摩擦力与重力的影响)
质量m=1吨的汽车通过圆形拱形桥时的速率恒定,拱形桥的半径R=5m。试求: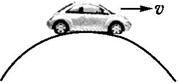
(1)汽车在最高点对拱形桥的压力为车重的一半时汽车的速度；
(2)汽车在最高点对拱形桥的压力为零时汽车的速度。
将一个物体以10m/s的速度从45m的高度水平抛出，试求：
（1）物体在空中运动的时间；
（2）物体落地时的速度大小；
（3）物体落地点离抛出点的水平距离。
如图所示，在xOy平面内有一范围足够大的匀强电场，电场强度大小为E，电场方向在图中未画出．在y≤l的区域内有磁感应强度为B的匀强磁场，磁场方向垂直于xOy平面向里．一电荷量为+q、质量为m的粒子，从O点由静止释放，运动到磁场边界P点时的速度刚好为零，P点坐标为（l，l），不计粒子所受重力．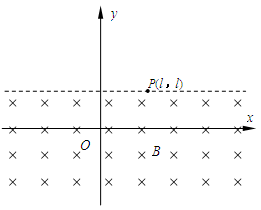 
（1）求从O到P的过程中电场力对带电粒子做的功，并判断匀强电场的方向．
（2）若该粒子在O点以沿OP方向、大小
的初速度开始运动，并从P点离开磁场，此过程中运动到离过OP的直线最远位置时的加速度大小
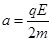，则此点离OP直线的距离是多少？
（3）若有另一电荷量为-q、质量为m的粒子能从O点匀速穿出磁场，设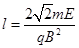
，求该粒子离开磁场后到达y轴时的位置坐标．
如图所示，在倾角为θ的斜面上放置一内壁光滑的凹槽A，凹槽A与斜面间的动摩擦因数μ＝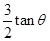
，槽内紧靠右挡板处有一小物块B，它与凹槽左挡板的距离为d．A、B的质量均为m，斜面足够长．现同时由静止释放A、B，此后B与A挡板每次发生碰撞均交换速度，碰撞时间都极短．已知重力加速度为g．求：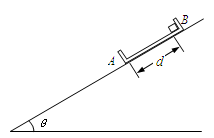
（1）物块B从开始释放到与凹槽A发生第一次碰撞所经过的时间t1．
（2）B与A发生第一次碰撞后，A下滑时的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2．
（3）凹槽A沿斜面下滑的总位移大小x．
如图所示，两根等高光滑的
圆弧轨道，半径为r、间距为L，轨道电阻不计．在轨道顶端连有一阻值为R的电阻，整个装置处在一竖直向上的匀强磁场中，磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑，到达轨道底端cd时受到轨道的支持力为2mg．整个过程中金属棒与导轨电接触良好，求：
（1）棒到达最低点时的速度大小和通过电阻R的电流．
（2）棒从ab下滑到cd过程中回路中产生的焦耳热和通过R的电荷量．
（3）若棒在拉力作用下，从cd开始以速度v0向右沿轨道做匀速圆周运动，则在到达ab的过程中拉力做的功为多少？