如图所示为学校操场上一质量不计的竖直滑杆，滑杆上端固定，下端悬空，为了研究学生沿杆的下滑情况，在杆的顶部装有一拉力传感器，可显示杆顶端所受拉力的大小，现有一学生（可视为质点）从上端由静止开始滑下，5 s末滑到杆底时速度恰好为零，从学生开始下滑时刻计时，传感器显示拉力随时间变化情况如图所示，g取10 m/s2，求：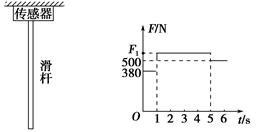
（1）该学生下滑过程中的最大速率；
（2）图中力F1的大小；
（3）滑杆的长度．
如图所示装置中，区域I和Ⅲ中分别有竖直向上和水平向右的匀强电场，电场强度分别为E和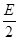
；Ⅱ区域内有垂直纸面向外的水平匀强磁场，磁感应强度为B。一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度V0水平射人电场，经水平分界线OP上的A点与OP成600角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的匀强电场中。求：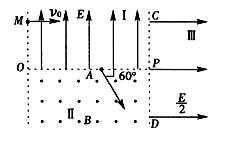
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径
(2)O、M间的距离
(3)粒子从M点出发到第二次通过CD边界所经历的时间
如图所示，在光滑绝缘的水平面内，对角线AC将边长为L的正方形分成ABC和ADC两个区域，ABC区域有垂直于水平面的匀强磁场，ADC区域有平行于DC并由C指向D的匀强电场．质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域，从对角线AC的中点O进入电场区域．
（1）判断磁场的方向并求出磁感应强度B的大小．
（2）讨论电场强度E在不同取值时，带电粒子在电场中运动的时间t．
如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的
．已知木块与地面的动摩擦因素μ=
，重力加速度取g．求：
（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离
静止在匀强磁场中的放射性原子核X发生衰变，衰变后带电粒子运动速度和磁感线垂直，两轨迹圆半径之比
，带电粒子在轨迹圆上运动的周期之比
。设衰变过程释放的核能全部转化成射线粒子和反冲核的动能，已知该衰变过程前后原子核的质量亏损为m。
(1)该衰变为衰变。(填“
”或“
”)
(2)写出核反应方程(反冲核的元素符号可用Y表示)：。
(3)计算射线粒子和反冲核的动能。
“人造太阳”并不是像太阳一样悬挂在天空，而是建造在地球上的受控热核聚变反应堆或核聚变电站，它能像太阳一样通过核聚变反应放出能量，进而发电，在合肥科学岛，我国最新一代核聚变实验装置“EAST”首次成功获得电流超过200 kA．时间近3 s的高温等离子放电，人造太阳能来自下面的反应：4个质子(氢核)聚变成1个a粒子，同时发射2个正电子和2个没有静止质量的中微子，“人造太阳”的总功率为P，质子、氢核、正电的质分别为，真空中的光速为c．
(1)写出核反应方程；
(2)求核反应所释放的能量△E
(3)求在时间内参与上述热核反应的质子数目。