已知以点C为圆心的圆经过点A(3,1)和B(1,3),且圆自身关于直线 对称.设直线
对称.设直线 :
: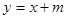 .
.
(1)求圆C的方程;
(2)在圆C上,若到直线 :
: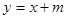 的距离等于1的点恰有4个,求
的距离等于1的点恰有4个,求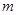 的取值范围.
的取值范围.
如图,矩形ABCD的两条对角线相交于点M(3,5),AB边所在直线的方程为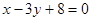 ,点N(0,6)在AD边所在直线上.
,点N(0,6)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求对角线AC所在直线的方程.
已知圆 :
: ,点
,点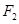 (1, 0),点
(1, 0),点 在圆
在圆 上运动,
上运动,  的垂直平分线交
的垂直平分线交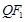 于点
于点 .
.
(1) 求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设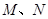 分别是曲线
分别是曲线 上的两个不同点,且点
上的两个不同点,且点 在第一象限,点
在第一象限,点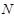 在第三象限,若
在第三象限,若 ,
, 为坐标原点,求直线
为坐标原点,求直线 的斜率;
的斜率;
(3)过点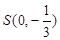 的动直线
的动直线 交曲线
交曲线 于
于 两点,求证:以
两点,求证:以 为直径的圆恒过定点
为直径的圆恒过定点
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:区间[100,110)的中点值为 =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
设命题 :函数
:函数 的定义域为
的定义域为 ;命题
;命题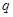 :当
:当 时,函数
时,函数 恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求
恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求 的取值范围.
的取值范围.