把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点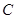
顺时针旋转
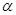角， 旋转后的矩形记为矩形
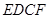．在旋转过程中，（1）如图①，当点E在射线CB上时，E点坐标为 ；
（2）当
是等边三角形时，旋转角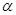的度数是 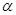（为锐角时）；（3）如图②，设EF与BC交于点G，当EG=CG时，求点G的坐标．
(4) 如图③，当旋转角
时，请判断矩形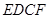的对称中心H是否在以C为顶点，且经过点
A的抛物线上．
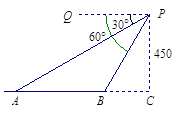
. 汶川地震后，抢险队派一架直升飞机去A、B两个村庄抢险，飞机在距地面450米上空的P点，测得A村的俯角为
，B村的俯角为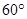
．（如图）．求A、B两个村庄间的距离．（结果精确到米，参考数据
）
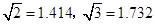已知:如图,在△ABC中，AD⊥BC于点D，CE⊥AB于点E，BE=2AE，且AD=
，sin∠BCE=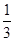
. 求CE的长.
已知二次函数
的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）．
（1）求此二次函数的解析式；
（2）求此二次函数的图象与x轴的另一个交点的坐标；
（3）根据图象回答：当x取何值时，y＜0？
已知二次函数
的图象经过点（1，0）和（-5，0）两点，顶点纵坐标为
，求这个二次函数的解析式。
如图，过□ABCD中的三个顶点A、B、D作⊙O，且圆心O在□ABCD的外部，AB=8，OD⊥AB于点E，⊙O的半径为5，求□ABCD的面积.