在平面直角坐标系 中,以点A(3,0)为圆心,5为半径的圆与
中,以点A(3,0)为圆心,5为半径的圆与 轴相交于点
轴相交于点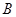 、
、 (点B在点C的左边),与
(点B在点C的左边),与 轴相交于点D、M(点D在点M的下方).
轴相交于点D、M(点D在点M的下方).(1)求以直线x=3为对称轴,且经过D、C两点的抛物线的解析式;
(2)若E为直线x=3上的任一点,则在抛物线上是否存在
这样的点F,使得以点B、C、E、F为顶点的四边形是平
行四边形?若存在,求出点F的坐标;若不存在,说明理由.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP=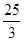 ,求AC的长.
,求AC的长.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.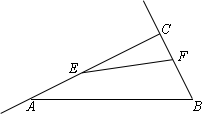
(1)填空:AB=cm;
(2)若0<t<5,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(3)若∠ACB的平分线CG交△ECF的外接圆于点G.试探究在整个运动过程中,CE、CF、CG之间存在的数量关系,并说明理由.
如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)