如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.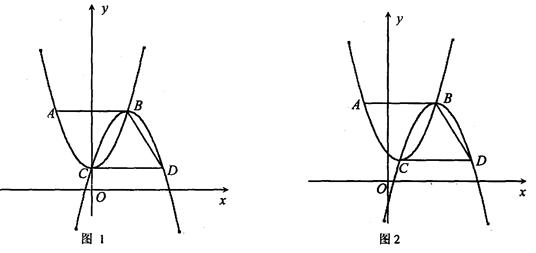
(1)求点A的坐标:
(2)如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;
(3)如图2,若将抛物线C1:“y1=x2+1”改
 为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 ▲ (直接写结果).
为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 ▲ (直接写结果).
计算:(每题3分,共18分)
(1)-20+(-14)-(-18)-13
(2)-(-28)÷(―6+4)+(―1)× ︳-5 ︳
(3)
(4)
(5)5m-7n-8p+5n-9m-p
(6)
在△ABC中, AB、BC、AC三边的长分别为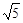 、
、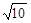 、
、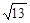 ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为:.
(2)若△DEF三边的长分别为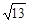 、
、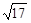 、
、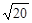 ,请在图2的正方形网格中画出相应的
,请在图2的正方形网格中画出相应的
△DEF,并利用构图法求出它的面积为_____________.
(3)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(4)如图4,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13m2、25m2、36m2,则六边形花坛ABCDEF的面积是m2.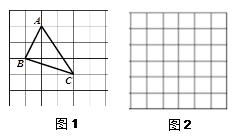

如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC= .现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
如图,直角三角形的两直角边AC="6" cm,BC="8" cm,沿AD折叠使AC落在AB上.点C与E重合,折痕为AD,试求CD的长.
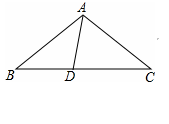
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.