( 12分)如图,在多面体 中,
中, 面
面 ,
, ,且
,且 ,
,
 为
为 中点。
中点。
(1)求证: 平面
平面 ;
;
(2)求平面 和平面
和平面 所成的锐二面角的余弦值。
所成的锐二面角的余弦值。
已知函数
(1)若曲线 在
在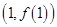 处的切线与x轴平行,求函数
处的切线与x轴平行,求函数 的单调区间;
的单调区间;
(2)当 的最大值大于
的最大值大于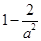 时,求a的取值范围.
时,求a的取值范围.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
(1)求证:PC⊥AD;
(2)求点D到平面PAM的距离.
为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:女生:
| 睡眠时间(小时) |
[4,5) |
[5,6) |
[6,7) |
[7,8) |
[8,9] |
| 人数 |
2 |
4 |
8 |
4 |
2 |
男生:
| 睡眠时间(小时) |
[4,5) |
[5,6) |
[6,7) |
[7,8) |
[8,9] |
| 人数 |
1 |
5 |
6 |
5 |
3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取3人,求此3人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2x2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
| 睡眠时间少于7小时 |
睡眠时间不少于7小时 |
合计 |
|
| 男生 |
|||
| 女生 |
|||
| 合计 |
P(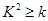 ) ) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.8879 |
10.828 |
( ,其中n=a+b+c+d)
,其中n=a+b+c+d)
已知数列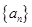 的前n项和为
的前n项和为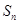 ,点
,点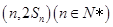 均在函数
均在函数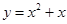 的图象上;
的图象上;
(1)求数列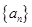 的通项公式;
的通项公式;
(2)设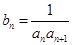 ,求数列
,求数列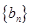 的前n项和
的前n项和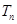
如图,椭圆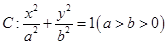 的离心率为
的离心率为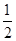 ,其左焦点到点
,其左焦点到点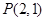 的距离为
的距离为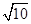 .不过原点
.不过原点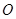 的直线
的直线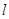 与
与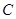 相交于
相交于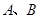 两点,且线段
两点,且线段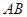 被直线
被直线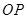 平分.
平分.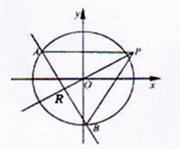
(1)求椭圆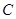 的方程;
的方程;
(2)求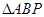 的面积取最大值时直线
的面积取最大值时直线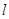 的方程.
的方程.