设 表示三条不同的直线,
表示三条不同的直线, 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若 ,则
,则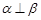 ;
;
②若 ,
, 是
是 在
在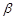 内的射影,
内的射影, ,则
,则 ;
;
③若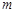 是平面
是平面 的一条斜线,
的一条斜线,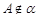 ,
, 为过
为过 的一条动直线,则可能有
的一条动直线,则可能有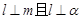 ;
;
④若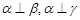 ,则
,则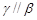
其中真命题的个数为( )个
| A.1 | B.2 | C.3 | D.4 |
已知集合A={x|x>1},B={x|x<m},且A∪B=R,那么m的值可以是( )
| A.-1 | B.0 | C.1 | D.2 |
已知函数f(x)=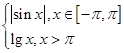 x1,x2,x3,x4,x5是方程f(x)=m的五个不等的实数根,则x1+x2+x3+x4+x5的取值范围是( )
x1,x2,x3,x4,x5是方程f(x)=m的五个不等的实数根,则x1+x2+x3+x4+x5的取值范围是( )
| A.(0,π) | B.(-π,π) | C.(lg π,1) | D.(π,10) |
已知x,y满足约束条件 若目标函数z=ax+y(其中a为常数)仅在点
若目标函数z=ax+y(其中a为常数)仅在点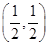 处取得最大值,则实数a的取值范围是( )
处取得最大值,则实数a的取值范围是( )
| A.(-2,2) | B.(0,1) |
| C.(-1,1) | D.(-1,0) |
已知点F1、F2分别是双曲线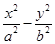 =1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
=1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
A.(1,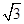 ) ) |
B.(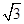 ,2 ,2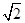 ) ) |
C.(1+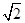 ,+∞) ,+∞) |
D.(1,1+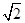 ) ) |
设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A.[1-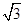 ,1+ ,1+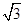 ] ] |
B.(-∞,1-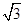 ]∪[1+ ]∪[1+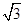 ,+∞) ,+∞) |
C.[2-2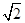 ,2+2 ,2+2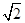 ] ] |
D.(-∞,2-2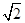 ]∪[2+2 ]∪[2+2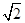 ,+∞) ,+∞) |