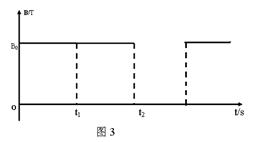
如图所示,水平放置的平行金属板a、b板长为L,板间距离为d。两板间所加电压变化情况如图2如示(U0已知)。两板间所加磁场的磁感应强度变化情况如图3所示(设磁感应强度方向垂直纸面向里为正,B0已知)。现有一质量为m,电荷量为q的带正电粒子,在t=0时刻沿平行金属板中轴线MN以某一初速度水平射入两板间,不计粒子重力。求: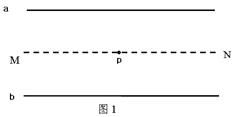

若在电场和磁场同时存在时(即0—t1时间内),粒子能沿直线MN运动,求粒子运动速度的大小。
若粒子能第二次通过中轴线中点P,且速度方向是竖直向下的,求电场和磁场同时存在的时间t1(粒子在此前运动过程中未与极板相碰)。
求在(2)中只有磁场存在的时间t2-t1的可能值。
如图所示,质量为0.78kg的金属块放在水平地面上,在大小为3.0N、方向与水平方向成370角的拉力F作用下,以4.0m/s的速度沿地面向右做匀速直线运动。已知sin370=0.6,cos370=0.8,g取10m/s2。求:
(1)金属块与地面间的动摩擦因数;
(2)如果从某时刻起撤去拉力F,此后金属块的加速度大小;
(3)撤去拉力F后金属块在地面上还能滑行多远?
如图所示,在竖直平面内,由斜面和圆形轨道分别与水平面相切连接而成的光滑轨道,圆形轨道的半径为R。质量为m的小物块从斜面上距水平面高为h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失。求:
⑴.小物块通过B点时速度vB的大小;
⑵.小物块通过圆形轨道最低点C时轨道对物块的支持力N的大小;
⑶.小物块能否通过圆形轨道的最高点D。
在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示。不计粒子重力,求
(1)画出粒子从M到P的运动轨迹示意图
(2)M、N两点间的电势差UMN;
(3)粒子在磁场中运动的轨道半径R;
(4)粒子从M点运动到P点的总时间t。
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.1m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=T.如果用此发电机带动两个标有“220V 11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如下图.求:
(1)发电机的输出电压的有效值为多少?
(2)变压器原副线圈的匝数比为多少?
(3)与变压器原线圈串联的交流电流表的示数为多少?
有一台发电机通过升压和降压变压器给用户供电,已知发电机的输出功率是20kW,端电压为500V,升压变压器原、副线圈的匝数比为n1﹕n2=1﹕5,两变压器之间输电导线的总电阻R=l0Ω,降压变压器输出电压U4=220V,求:
(1)升压变压器的输出电压;
(2)输电线上损失的电功率是多大;
(3)降压变压器的原、副线圈的匝数比n3﹕n4;