定义集合 ,若集合
,若集合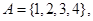 集合
集合 ,
,
则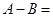 ( )
( )
| A.{1,2} | B.{3,4} |
C.{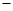 5, 5,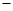 7} 7} |
D.{1,2,3,4,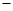 5, 5,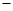 7} 7} |
已知函数f(x)=lg,若,则f(-a)=( )
| A.b | B.-b | C. | D.- |
如下图所示,面积为S的平面凸四边形的第i条边的边长记为ai,此四边形内任一点P到第i条边的距离记为hi,若====k,则=.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si,此三棱锥内任一点Q到第i个面的距离记为Hi,若====k,则=( )
| A. | B. | C. | D. |
给出下面类比推理命题(其中R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈C,则复数a+bi=c+di⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b”类比推出“若a,b∈C,则a-b>0⇒a>b”;
④“若a,b∈R,则a·b=0⇒a=0或b=0”.类比推出“若a,b∈C,则a·b=0⇒a=0或b=0”.
其中类比结论正确的个数是( )
| A.0 | B.1 |
| C.2 | D.3 |
设f0(x)=cos x,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N*,则f2011(x)=( )
| A.-sin x | B.-cos x |
| C.sin x | D.cos x |
凸n边形有f(n)条对角线,则凸n+1边形有f(n+1)条对角线数为( )
| A.f(n)+n-1 | B.f(n)+n |
| C.f(n)+n+1 | D.f(n)+n-2 |