已知直线l1:mx+8y+n=0与l2:2x+my-1=0互相平行,求过点(m,n)与 垂直并且被
垂直并且被 截得的线段长为
截得的线段长为 的直线方程。
的直线方程。
(本小题8分)根据下列条件写出直线的方程,并且化成—般式
(1)经过点 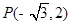 且倾斜角
且倾斜角 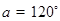 ;
;
(2)经过点A(-1,0)和B(2,-3).
(本小题6分)如图,已知—正三棱锥P- ABC的底面棱长AB=3,高PO= 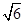 ,求这个正三棱锥的表面积.
,求这个正三棱锥的表面积.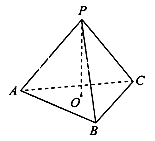
(本小题满分14分)已知函数 .
.
(1)求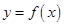 的定义域;
的定义域;
(2)在函数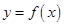 的图像上是否存在不同的两点,使过此两点的直线平行于
的图像上是否存在不同的两点,使过此两点的直线平行于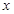 轴;
轴;
(3)当 满足什么关系时,
满足什么关系时, 在
在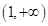 上恒取正值.
上恒取正值.
(本小题满分12分)
某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若最初时含杂质2%,每过滤一次可使杂质含量减少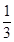 ,问至少应过滤几次才能使产品达到市场要求?
,问至少应过滤几次才能使产品达到市场要求?
(已知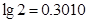 ,
, )
)
(本小题满分12分)如图,棱长为1的正方体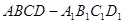 中,
中,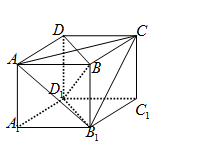
(1)求证: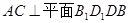 ;
;
(2) 求三棱锥 的体积.
的体积.