探究应用:(1)计算:(a-2)(a2 + 2a + 4)= 。
(2x-y)(4x2 +2xy+y2)= 。(2)上面的乘法计算结果很简洁,聪明的你又可以发现一个新的乘法公式,可以用含a,b的字母表示为 。
(3)下列各式能用你发现的乘法公式计算的是( )
| A.(a-3)(a2-3a+9) | B.(2m-n)(2m2+ 2mn + n2) |
C.(4-x) (16 + 4x + x2) (16 + 4x + x2) |
D.(m-n)(m2+ 2mn + n2) |
(4)直接用公式计算:(3x - 2y)(9x2 + 6xy + 4y2)= 。
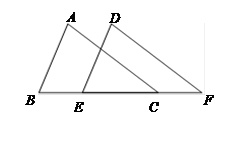
如图,已知点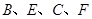 在同一直线上,
在同一直线上,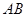 ∥
∥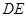 ,且
,且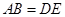 ,
,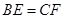 ,求证:
,求证: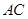 ∥
∥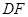 .
.
如下图,直线L是一条河,A,B是两个村庄。欲在L上的某处修建一个水泵站M,向A,B两地供水,作出水泵站M,使所需管道MA+MB的长最短。
(不写作法,保留作图痕迹)
(1)在左图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;(2)在右图中,画出与△ABC关于x轴对称的△A1B1C1。
(1)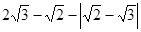 (2)
(2)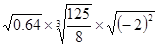
把一副三角板按如图甲放置,其中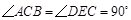 ,
,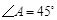 ,
,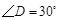 ,斜边
,斜边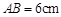 ,
, .把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点
.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点 、与D1E1相交于点F.
、与D1E1相交于点F.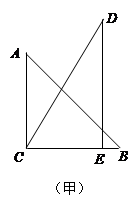
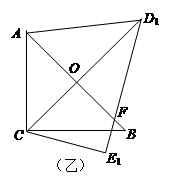
(1)求 的度数;
的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由。