如图8所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.以拱桥的最高点为原点建立如图的坐标系,求抛物线的解析式;
若洪水到来时,水位以每小时
 m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶.
m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶.
(1)如图1,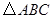 和
和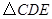 都是等边三角形,且
都是等边三角形,且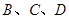 三点共线,连接
三点共线,连接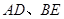 相交于点
相交于点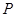 ,求证:
,求证: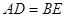 .
.
(2)如图2,在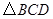 中,
中,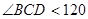 °,分别以
°,分别以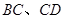 和
和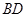 为边在
为边在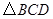 外部作等边
外部作等边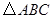 、等边
、等边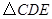 和等边
和等边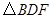 ,联结
,联结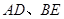 和
和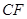 交于点
交于点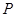 ,下列结论中正确的是 (只填序号即可)
,下列结论中正确的是 (只填序号即可)
①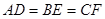 ;②
;② ;③
;③ °;
°;
(3)如图2,在(2)的条件下,求证: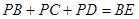 .
.
如图,四边形ABCD与四边形BEFG都是正方形,设AB=a,DE=b(a>b).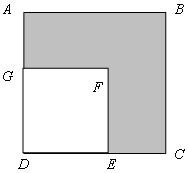
(1)写出AG的长度(用含字母a、b的代数式表示);
(2)观察图形,试用不同的方法表示图形中阴影部分的面积,你能获得相应的一个因式分解公式吗?请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2.试利用⑵中的公式,求a、b的值.
如图,在四边形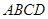 中,
中,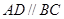 ,
,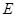 是
是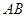 的中点,连接
的中点,连接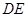 并延长交
并延长交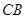 的延长线于点
的延长线于点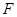 ,点
,点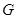 在
在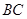 边上,且
边上,且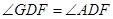 .
.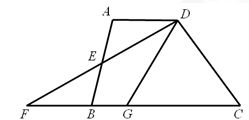
(1)求证: ;
;
(2)连接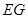 ,如果FM=DM,判断
,如果FM=DM,判断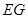 与
与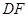 的位置关系,并说明理由.
的位置关系,并说明理由.
已知:如图,在△ABC中,∠A=120°,AB=BC,D是BC边的中点,DE⊥AB,DE⊥AC,点E,F为垂足.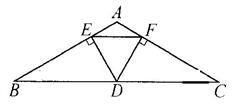
(1)求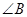 、
、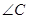 的度数;
的度数;
(2)求证: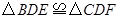 ;
;
(3)求证: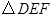 是等边三角形.
是等边三角形.
已知:Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、EB.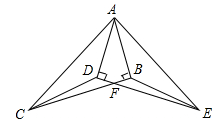
(1)请找出图中其他的全等三角形;
(2)求证:CD=EB;
(3)求证:CF=EF.