(本小题满分10分)选修4-1:几何证明选讲
如图,直线 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且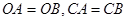 .⊙
.⊙ 交直线
交直线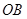 于
于 ,
, ,连接
,连接 .
.
(Ⅰ)求证:直线 是⊙
是⊙ 的切线;
的切线;
(Ⅱ)若 ,⊙
,⊙ 的半径为3,求
的半径为3,求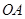 的长.
的长.
已知函数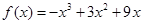
(Ⅰ)求曲线y=f(x)在(1,11)处的切线方程;(Ⅱ)求函数的单调区间
(Ⅲ)求函数在[-2,2]上的最值。
已知二次函数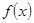 满足
满足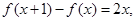 且
且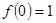 .
.
(Ⅰ)求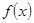 的解析式.(Ⅱ)在区间
的解析式.(Ⅱ)在区间 上,
上, 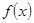 的图象恒在
的图象恒在 的图象上方 试确定实数
的图象上方 试确定实数 的范围.
的范围.
已知数列{xn}的首项x1=3,通项 (n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(n∈N+,p、q为常数)且x1,x4,x5成等差数列.
(Ⅰ)求p、q的值;(Ⅱ){xn}前n项和为Sn,计算S10的值.
在 中,
中,  所对边分别为
所对边分别为 .
.
已知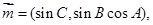
 ,且
,且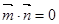 .
.
(Ⅰ)求 大小;(Ⅱ)若
大小;(Ⅱ)若 求
求 的面积S的大小.
的面积S的大小.
已知集合 的元素全为实数,且满足:若
的元素全为实数,且满足:若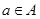 ,则
,则 。
。
(1)若 ,求出
,求出 中其它所有元素;
中其它所有元素;
(2)0是不是集合 中的元素?请你设计一个实数
中的元素?请你设计一个实数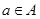 ,再求出
,再求出 中的所有元素?
中的所有元素?
(3)根据(1)(2),你能得出什么结论。