(14分
) 在光滑水平地面上，静止着一个质量为M =" 4" kg的小车．如图所示，在车的最右端有一个质量为m =" 1" kg的大小不计的物体，已
知物体与小车之间的动摩擦因数为0.2，小车的长度L =" 2" m，现在用恒定的水平力F =" 14" N向右拉动小车，求F拉动3s时，小车的速度多大？ （设最大静摩擦力等于滑动摩擦力）． (g =" 10" m/s2)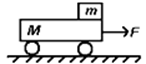
某金属导体两端的电压为24V，30s内有36C的电荷量通过导体的横截面，则：
（1）导体中的电流有多大？
（2）该导体的电阻多大？
（3）每秒钟内有多少个自由电子通过该导体的横截面？
如图所示，固定于同一条竖直线上的A.B是两个带等量异种电荷的点电荷，电荷量均为Q，其中A带正电荷，B带负电荷，D.C是它们连线的垂直平分线，A.B.C三点构成一边长为
的等边三角形。另有一个带电小球E，质量为
、电荷量为
（可视为点电荷），被长为L的绝缘轻质细线悬挂于O点，O点在C点的正上方。现在办小球E拉到M点，使细线水平绑紧且与A.B.C处于同一竖直面内，并由静止开始释放，小球E向下运动到最低点C时，速度为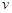
，已知静电力常量为
，重力加速度为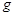
，试求：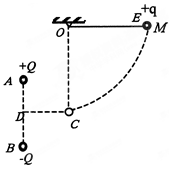
（1）带电小球E在C点所受的库仑力的大小及方向
（2）绝缘细线在C点对带电小球E的拉力T
（3）取D点的电势为零，求A.B所形成的电场中，M点的电势
。
套在长绝缘直棒上的小环质量为
，带电量为
，小环内径比棒的直径略大。将棒放置在方向均水平且正交的匀强电场和匀强磁场中，电场强度为E，磁感应强度为B，小环与棒的动摩擦因数为
，重力加速度为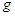
，现将小环从静止释放，小环可沿绝缘直棒下滑，棒足够长，求：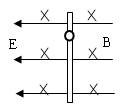
（1）小环从静止释放瞬间加速度
的大小
（2）小环运动过程的最大加速度
为多大，此时速度
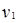为多大？
（3）小环运动过程张最大速度
为多大？
如图所示，水平放置的光滑的金属导轨M、N，平行地置于匀强磁场中，间距为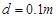
，金属棒
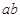的质量为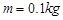
，电阻不计，放在导轨上且与导轨垂直。磁场的磁感应强度大小为
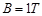，方向与导轨平面成夹角
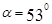且与金属棒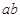垂直，定值电阻为
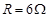，电源内阻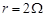
，当开关K闭合的瞬间，测得棒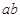的加速度大小为
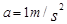，则电源电动势为多大？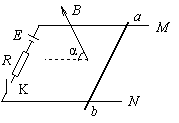
赤道附近的地磁场可以看作是沿南北方向的匀强磁场，磁感应强度的大小是0.5×10-4T。如果赤道上有一根沿东西方向的直导线长为20m，通有从东向西的电流30A，问：地磁场对这根导线的作用力有多大？方向如何？