如图,有6个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(4,0),O4(0,2),O5(2,2),O6(4,2).记集合M={⊙Oi|i=1,2,3,4,5,6}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中 “有序集合对”(A,B) 的个数是
| A.50 | B.54 | C.58 | D.60 |

抛物线C1:y= x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A. |
B. |
C. |
D. |
O为坐标原点,F为抛物线C:y2=4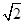 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4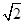 ,则△POF的面积为( ).
,则△POF的面积为( ).
| A.2 | B.2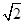 |
C.2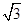 |
D.4 |
设椭圆C: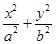 =1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).
=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).
A.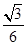 |
B.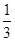 |
C. |
D.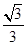 |
抛物线y2=4x的焦点到双曲线x2- =1的渐近线的距离是( ).
=1的渐近线的距离是( ).
A. |
B. |
C.1 | D.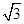 |
已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于 ,则C的方程是( ).
,则C的方程是( ).
A.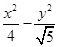 =1 =1 |
B.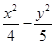 =1 =1 |
C.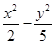 =1 =1 |
D. =1 =1 |