(本题12分)如图,已知抛物线y=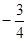 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=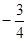 x+b相交于点B、C,直线y=
x+b相交于点B、C,直线y=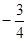 x+b与y轴交于点E.
x+b与y轴交于点E.
(1)写出直线BC的解析式;
(2)求△ABC的面积;
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A、B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积s与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?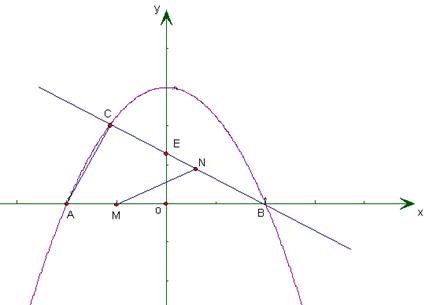
一辆汽车行驶时的耗油量为0.1升 千米,如图是油箱剩余油量 (升 关于加满油后已行驶的路程 (千米)的函数图象.
(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.

为了解某地区机动车拥有量对道路通行的影响,学校九年级社会实践小组对2010年 年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计,并绘制成下列统计图:

根据统计图,回答下列问题:
(1)写出2016年机动车的拥有量,分别计算2010年 年在人民路路口和学校门口堵车次数的平均数.
(2)根据统计数据,结合生活实际,对机动车拥有量与人民路路口和学校门口堵车次数,说说你的看法.
如图, 的直角边 在 轴上,顶点 的坐标为 ,直线 交 于点 ,交 轴于点 .
(1)求直线 的函数表达式;
(2)动点 在 轴上从点 出发,以每秒1个单位的速度向 轴正方向运动,过点 作直线 垂直于 轴,设运动时间为 .
①点 在运动过程中,是否存在某个位置,使得 ,若存在,请求出点 的坐标;若不存在,请说明理由;
②请探索当 为何值时,在直线 上存在点 ,在直线 上存在点 ,使得以 为一边, , , , 为顶点的四边形为菱形,并求出此时 的值.

某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为 轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

如图,已知 为 直径, 是 的切线,连接 交 于点 ,取 的中点 ,连接 交 于点 ,过点 作 于 .
(1)求证: ;
(2)若 , ,求 和 的长.
