下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据:
(吨)的几组对应数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
 |
4 |
4.5 |
根据上表提供的数据,求出 关于
关于 的线性回归方程为
的线性回归方程为 ,那么表中
,那么表中 的值为
的值为
A、4.5
B、3.5
C、3.15
D、3
设有一个直线回归方程为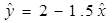 ,则变量
,则变量 增加一个单位时( )
增加一个单位时( )
A.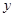 平均增加1.5个单位 平均增加1.5个单位 |
B.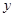 平均增加2个单位 平均增加2个单位 |
C.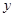 平均减少 1.5个单位 平均减少 1.5个单位 |
D.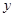 平均减少2个单位 平均减少2个单位 |
下列对一组数据的分析,不正确的说法是( )
| A.数据极差越小,样本数据分布越集中、稳定 |
| B.数据平均数越小,样本数据分布越集中、稳定 |
| C.数据标准差越小,样本数据分布越集中、稳定 |
| D.数据方差越小,样本数据分布越集中、稳定 |
下列程序框中,出口可以有两个流向的是( )
| A.终止框 | B.输入输出框 | C.处理框 | D.判断框 |
函数 定义域为R,且对任意
定义域为R,且对任意
 ,
, 恒成立.则下列选项中不恒成立的是
恒成立.则下列选项中不恒成立的是
A. |
B. |
C. |
D. |
方程 的实数解所在的区间是
的实数解所在的区间是
A. |
B. |
C. |
D. |