(本小题满分14分)已知数列 的前
的前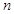 项和为
项和为 ,点
,点 在直线
在直线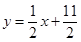 上;数列
上;数列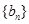 满足
满足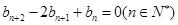 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、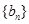 的通项公式;
的通项公式;
(2)设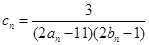 ,数列
,数列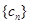 的前
的前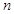 项和为
项和为 ,求使不等式
,求使不等式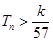 对一切
对一切 都成立的最大正整数
都成立的最大正整数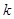 的值;
的值;
(3)设 ,是否存在
,是否存在 ,使得
,使得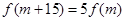 成立?若存在,求出
成立?若存在,求出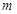 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,四棱锥 的底面是正方形,侧棱
的底面是正方形,侧棱 ⊥平面
⊥平面 ,
, 、
、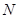 分别是
分别是 、
、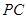 的中点.
的中点.
(1)求证: 平面
平面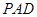 ;
;
(2)求证: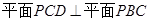 .
.
某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 |
乙 |
|
| 9 8 |
8 |
4 8 9 |
| 2 1 0 |
9 |
 6 6 |
(1)求 ;
;
(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份试卷中,求至多有一份得分在 之间的概率.
之间的概率.
为了更好的开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”, “街舞”, “动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表(单位:人)
| 社团 |
相关人数 |
抽取人数 |
| 模拟联合国 |
24 |
 |
| 街舞 |
18 |
3 |
| 动漫 |
 |
4 |
| 话剧 |
12 |
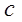 |
(1)求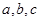 的值;
的值;
(2)若从“动漫”与“话剧”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
已知函数 的图象经过点
的图象经过点 .
.
(1)求实数 的值;
的值;
(2)求函数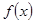 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
已知函数 .
.
(1)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(2)若 ,且对于任意
,且对于任意 ,
,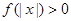 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)设函数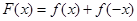 ,求证:
,求证: .
.