(本小题满分12分)设点P的坐标为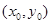 ,直线l的方程为
,直线l的方程为 .请写出点P到直线l的距离,并加以证明.
.请写出点P到直线l的距离,并加以证明.
如图,在四棱锥 中,底面
中,底面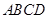 为平行四边形,
为平行四边形, ,
, ,
,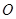 为
为 中点,
中点,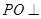 平面
平面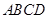 ,
,  ,
,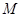 为
为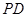 中点.
中点.
(1)证明: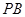 //平面
//平面 ;
;
(2)证明: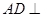 平面
平面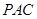 ;
;
(3)求直线 与平面
与平面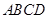 所成角的正切值.
所成角的正切值.
已知向量
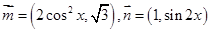 ,函数
,函数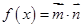
(1)求函数 的单调增区间;
的单调增区间;
(2)在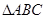 中,
中, 分别是角A, B, C的对边,且
分别是角A, B, C的对边,且 ,且
,且
求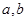 的值.
的值.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: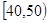 ,
,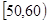 ,…,
,…,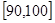 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.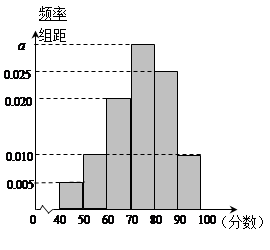
(1)求图中实数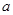 的值;
的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在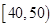 与
与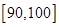 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
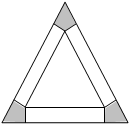
把边长为 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为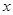 ,容积为
,容积为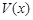 .
.
(Ⅰ)写出函数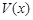 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(Ⅱ)求当x为多少时,容器的容积最大?并求出最大容积.
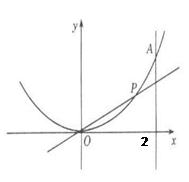
设点P在曲线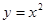 上,从原点向A(2,4)移动,如果直线OP,曲线
上,从原点向A(2,4)移动,如果直线OP,曲线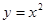 及直线x=2所围成的面积分别记为
及直线x=2所围成的面积分别记为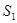 、
、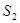 。
。
(Ⅰ)当 时,求点P的坐标;
时,求点P的坐标;
(Ⅱ)当 有最小值时,求点P的坐标和最小值.
有最小值时,求点P的坐标和最小值.